关于微信公众号

[TOC]

这篇文章参考了知乎上 Steven Yue 文章的内容，他的 Lattice 学习笔记 和 格密码学进阶 系列文章很值得阅读！我的文章可能偏 CTF 一点，一些理论性质介绍得也比较“简陋”。相较而言他的文章则更加学术、严谨、全面一些。

SVP问题（Shortest Vector Problem）

顾名思义，最短向量问题（SVP，Shortest Vector Problem）就是在格中找到“长度”最短的向量。为了方便理解，我们就把其中的一个点设置成坐标轴 0 点。这样问题就变成了找到距离 0 点最近的格点 $B_x$

一般我们使用向量的欧几里得范数作为“距离”的定义。

定义：对于 $n$ 维向量 $v$ 的欧几里得范数为 $||v||=\sqrt{v_1^2+v_2^2+\cdots+v_n^2}$

我们可以用 $\lambda $ 来定义整个格中点与点之间最短的距离。

对于 $n$ 维的格，因为一个格基由 $n$ 条向量组成，相应的就会有 $n$ 条最短的向量 $\lambda_1,\lambda_2,\dots,\lambda_n$ 其中我们设 $\lambda_1 \le \lambda_2 \le \cdots \le \lambda_n$ 。

下图展示了一个 2 维格的最短两条向量 $\lambda_1,\lambda_2$

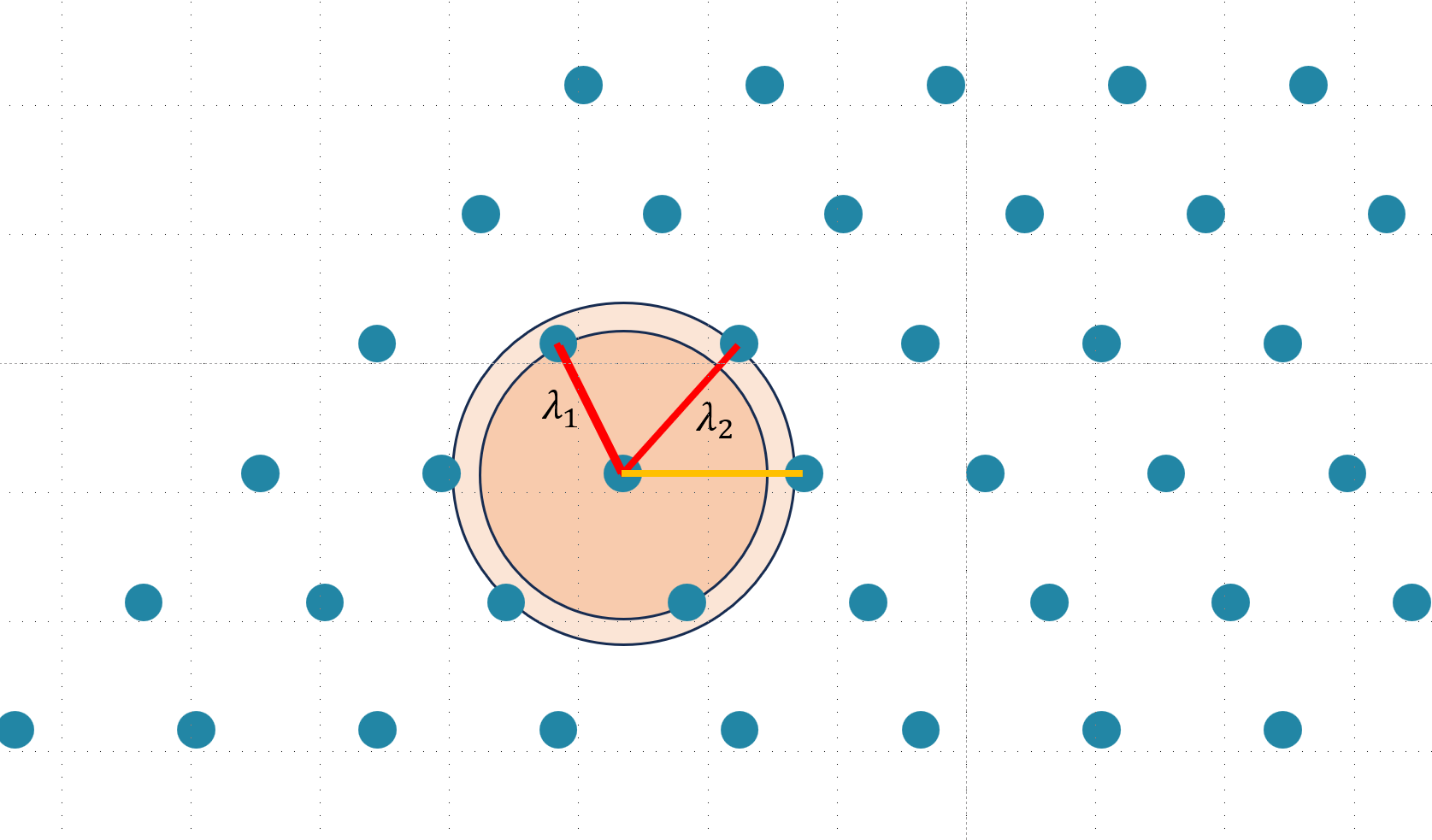
上图中，我们尚可以根据所画同心圆的半径来判断，黄色线条所表示向量的长度是大于 $\lambda_1,\lambda_2$ 的。但如果维度上去了，我们无法作图，该如何找到格中最短的向量呢？

一个很直观的想法，如果我们手上的格基是相互正交的，那么我们只需要遍历格基中的各个向量就可以找到最短的向量了。

于是我们就发现了这个惊天秘密：为了找到最短向量，就要尽量使得格基正交。

CVP问题（Closest Vector Problem）

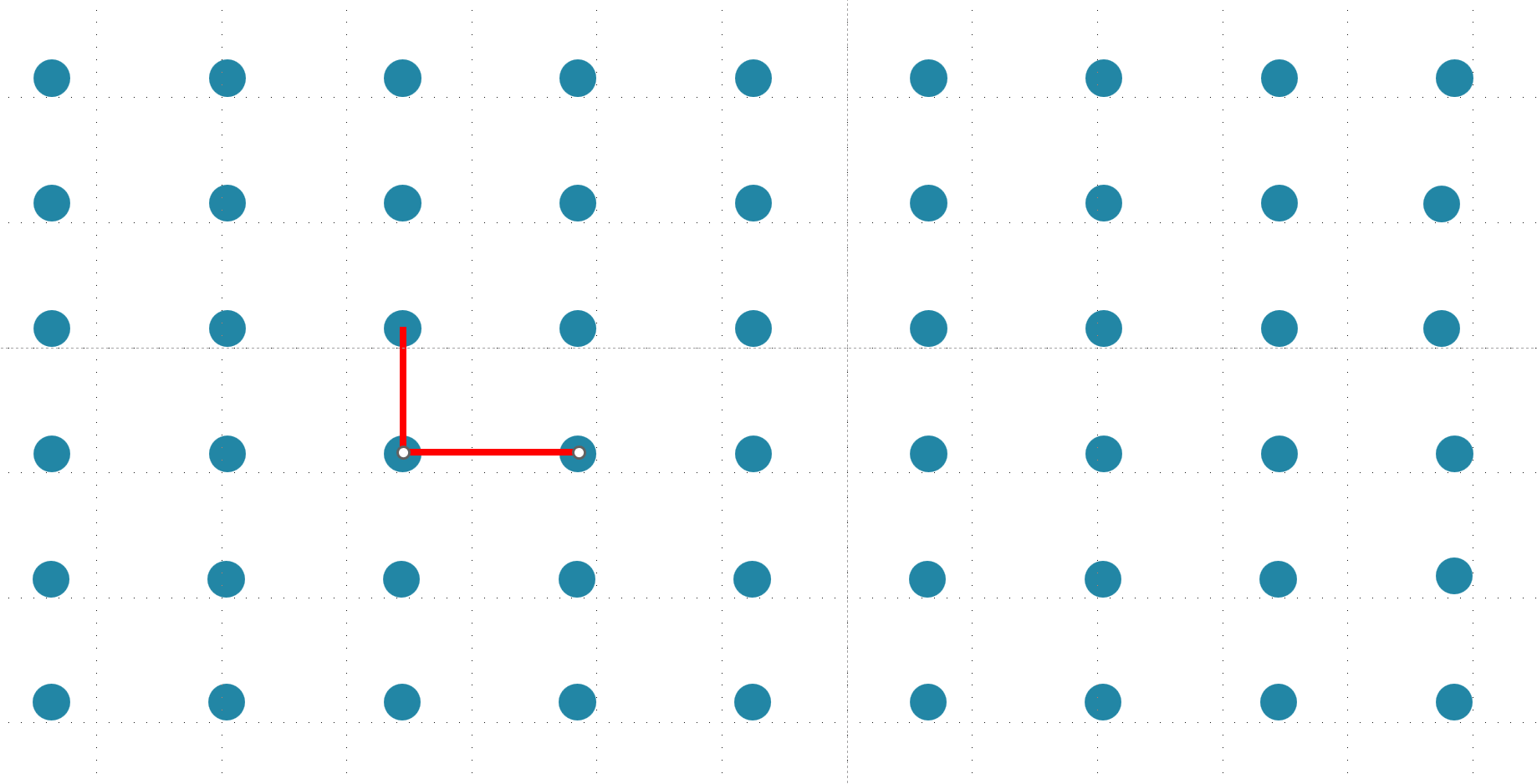
Lattice中另一大问题就是最近向量问题（CVP，Closest Vector Problem）了。问题的定义是这样的：给定连续空间中任意的一个点 $t$ ，找到距离这个点最近的格点 $Bx$。

其余包括还有 SIVP问题（Shortest Independent Vectors Problem）,BDD（Bounded Distance Decoding）问题 ,ADD（Absolute Distance Decoding）问题 ** 等都是 **SVP, CVP 的衍生，可以搞出如下的关联性

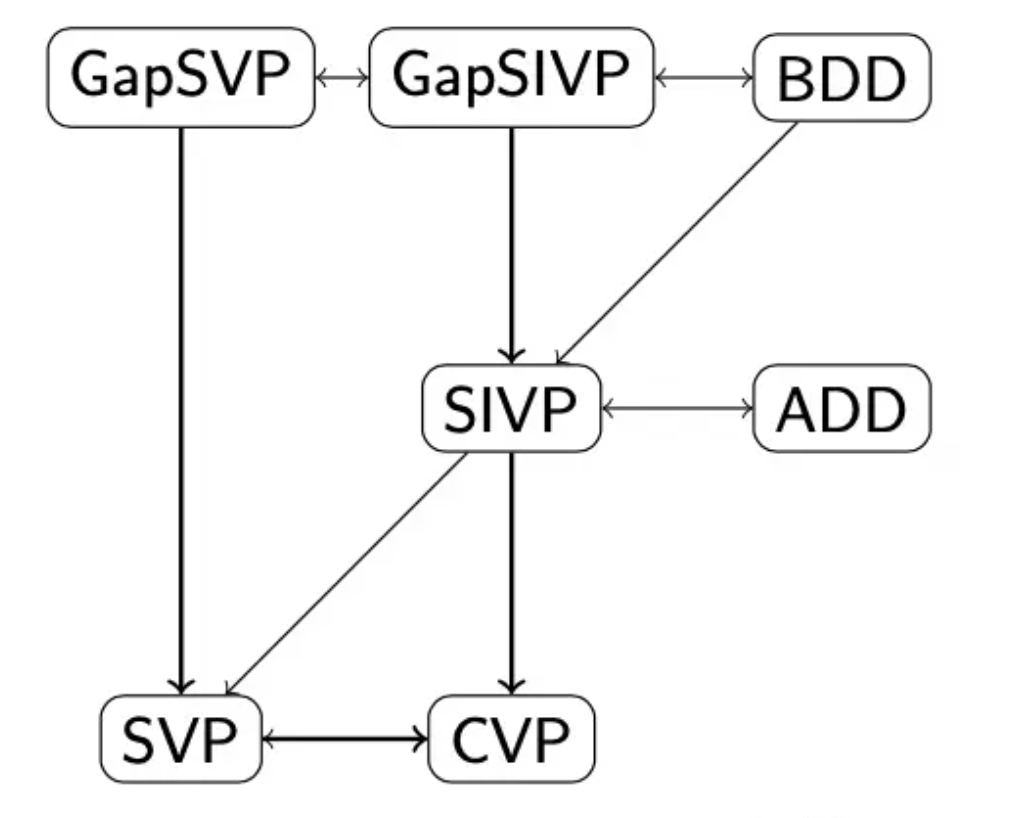
虽然最近二三十年来的各种paper逐渐的把这些难度的关系给证明了出来，但是对于我这个打比赛的粗鄙之人而言，他们都没啥区别。因为竞赛中的题目很难准确的控制好这个度，而一旦度没有控制好，使得我能够直接解决 SVP，那不管是其他什么 P 我都能够一把梭梭掉。

下面我们举个例子来说明如何将 CVP 转化为 SVP，从而通过解决 SVP 来解决 CVP。（可能会有读者疑惑，解决 CVP 就解决 CVP，干嘛非得转化乘成 SVP ？呃，这么说吧，如果能够一招鲜吃遍天，那何乐而不为呢？另外就是因为日益增长的攻击手法和笔者不太够的脑容量之间的矛盾）

CVP → SVP

为了方便演示，假设我们有一个一维的格，然后我们需要找到距离点 $t$ 最近的格点 $B_x$

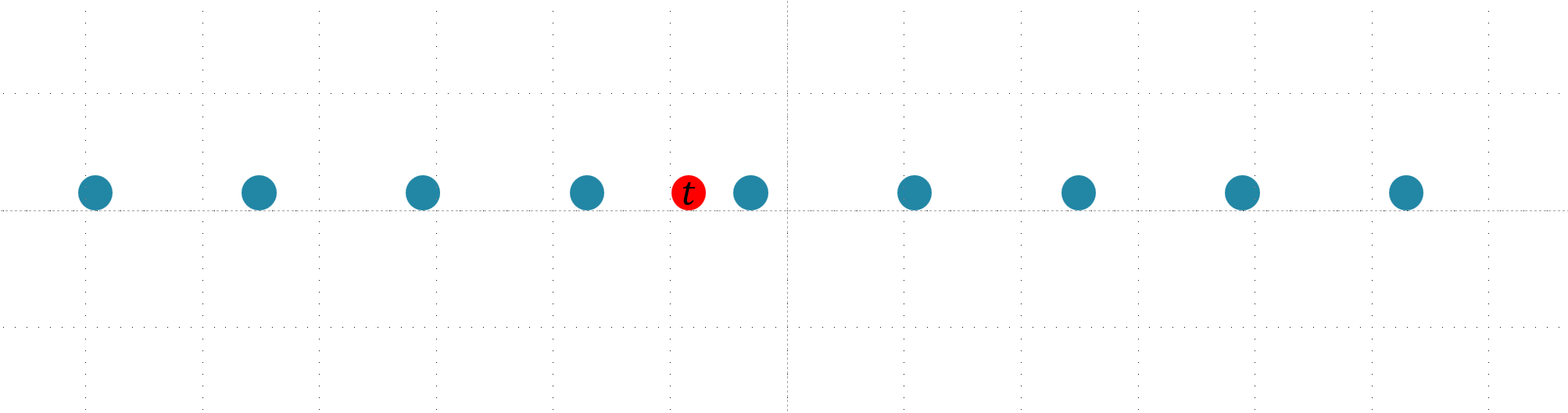
那么我们可以进行一个类似于“升维”的操作，使得 $t$ 点也成为新格的一个格点。

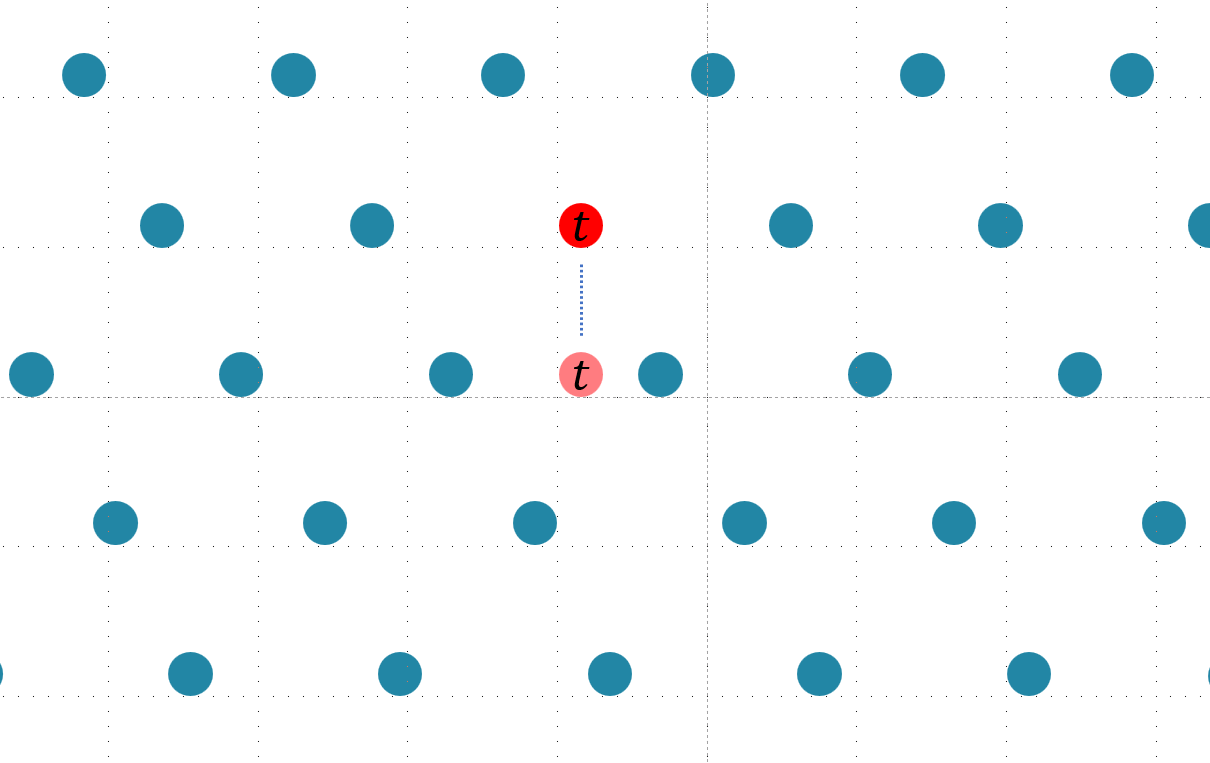
然后在这个新格中我们解决一下 SVP，找到最短向量，然后再将这个最短向量投影回原来的低维中，我们就能找到原来格中距离 $t$ 最近的格点 $Bx$ 了。

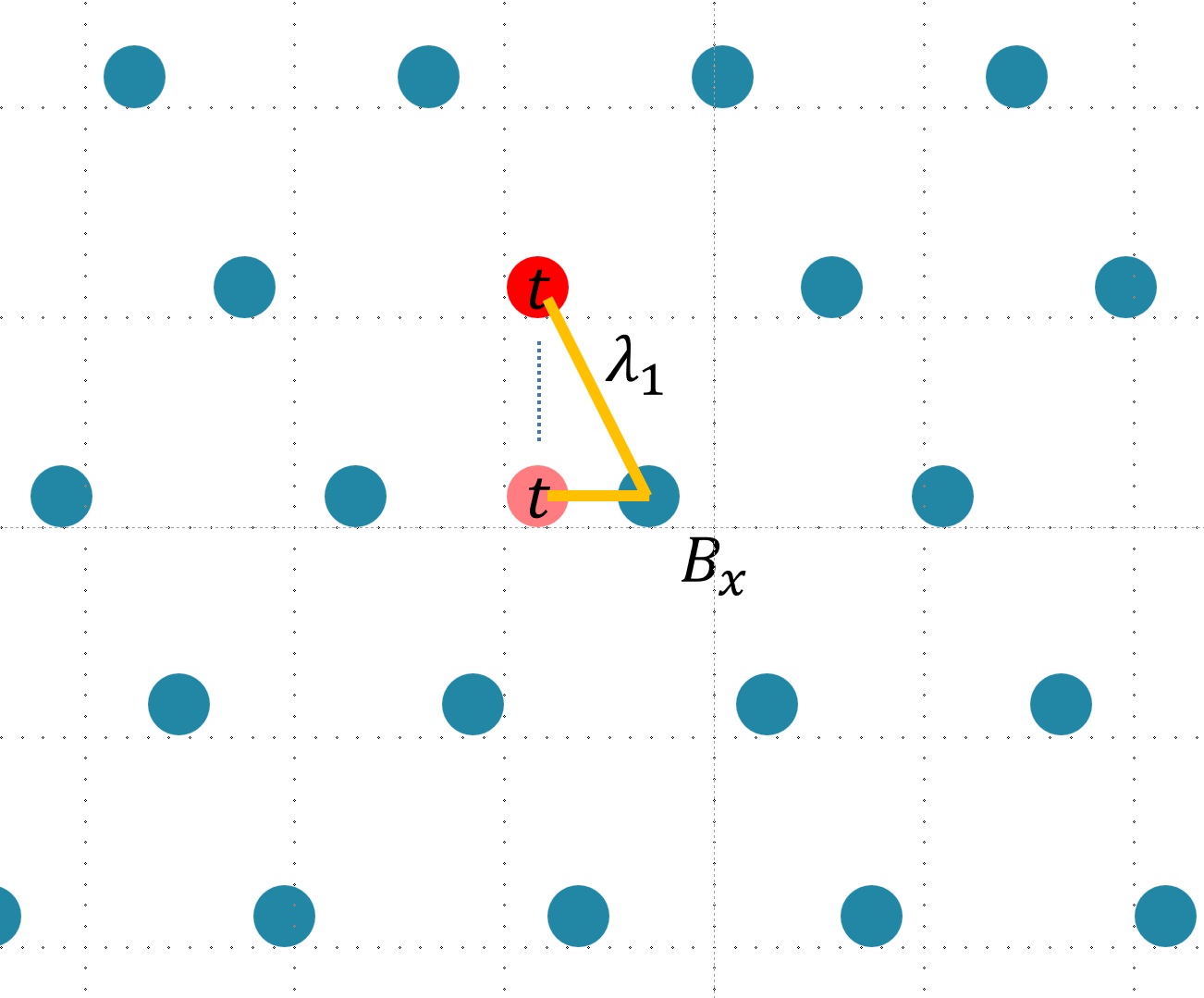
于是压力来到解决 SVP 这边，而我们之前也说了，“为了找到最短向量，就要尽量使得格基正交”，于是压力又来到 找到正交基 这边。

Gram-Schmidt正交化

事实上，由于“离散”的特性，我们仅可以通过对格基进行一系列（系数为整数）的线性变换找到接近正交的基，而这一过程，我们称为格基规约（Lattice Basis Reduction）

这里我们先介绍一种在线性代数中会学到的规约方法，即 Gram-Schmidt正交化，方便起见，我们在二维格上进行演示。

假设我们拥有一组基 $B = [b_1,b_2]$

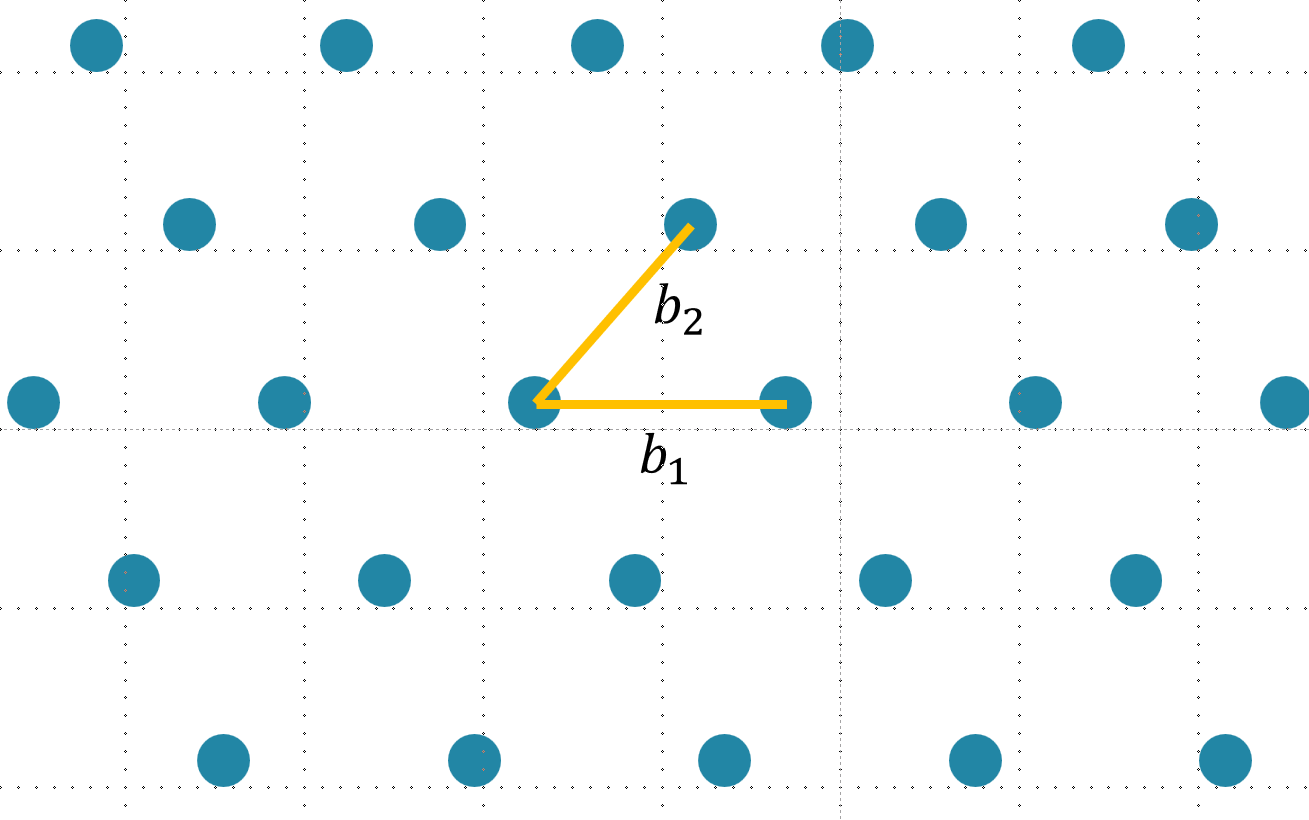
在这个Lattice中，这两个基向量是不垂直的。接下来，我们尝试找到一组互相垂直的基满足 $b_1^* \perp b_2^$。垂直是相互，所以我们先设 $b_1^ = b_1$，然后尝试去找 $b_2^*$

那么 $b_2^$ 就是原本的 $b_2$ 和 $b_1$ 的任意（这里先任意一下）线性组合，我们把这个取值范围用一条线来表示。在这个范围上变化，$b_2^$ 和 $b_1^*$ 所表示的格基的 Determinant 是不变的。

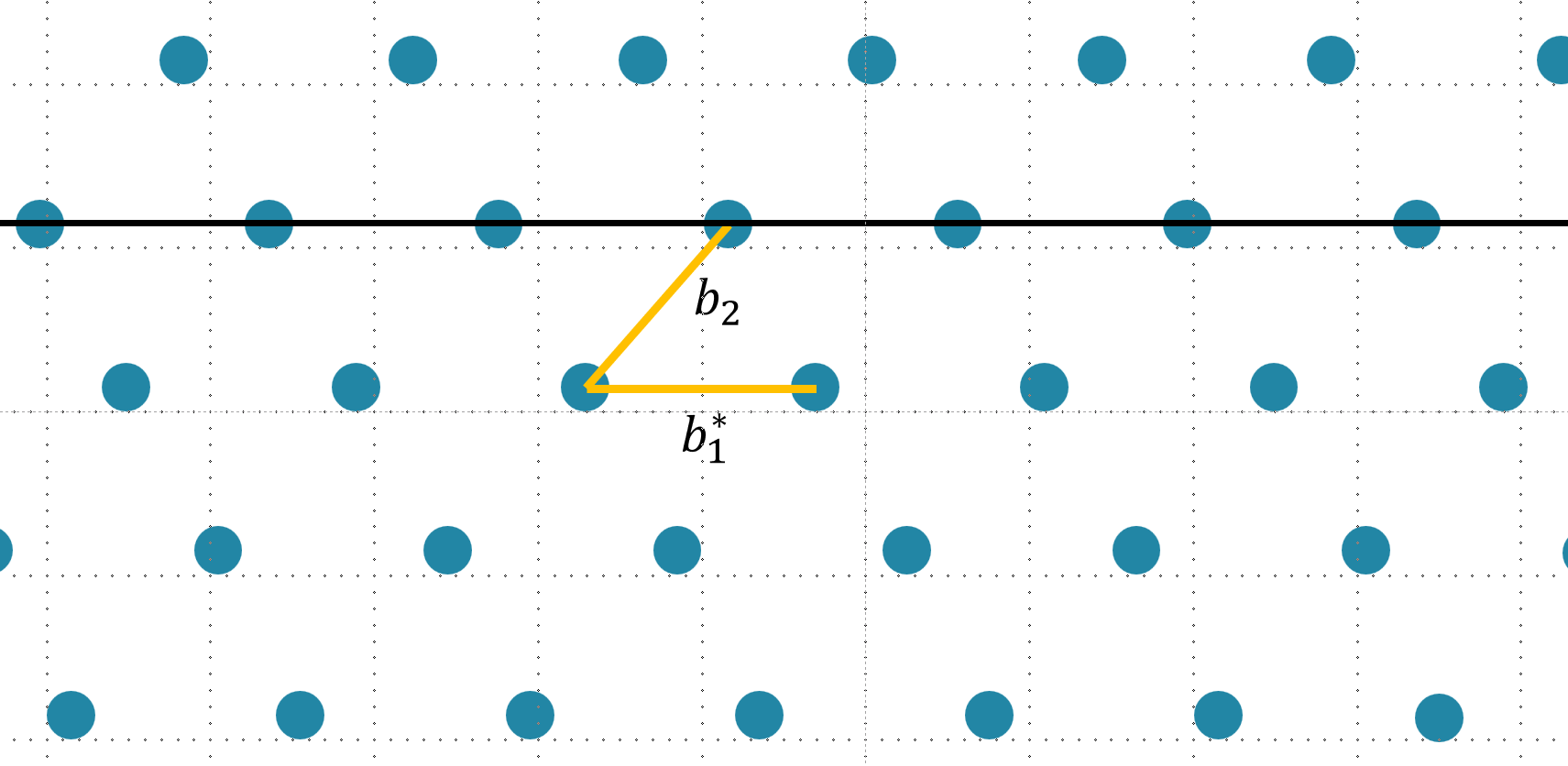
那么我们就可以选取一个与 $b_1^$ 垂直的向量作为 $b_2^$

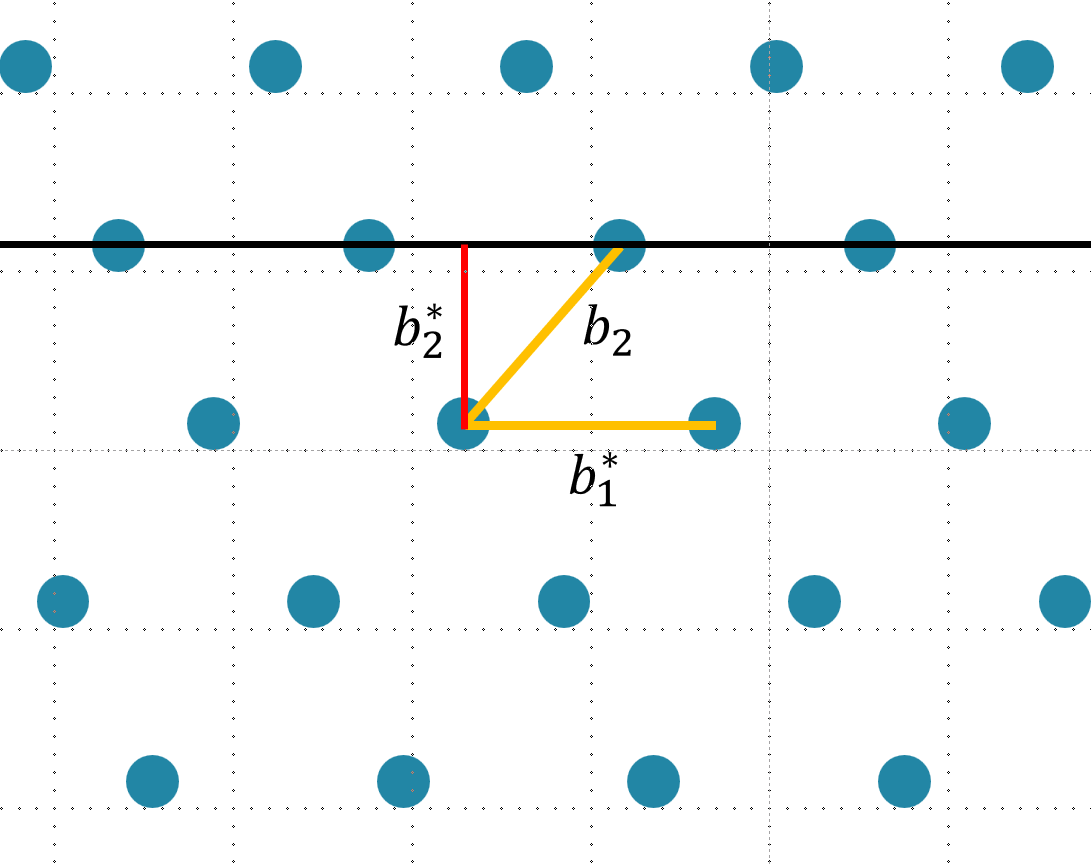
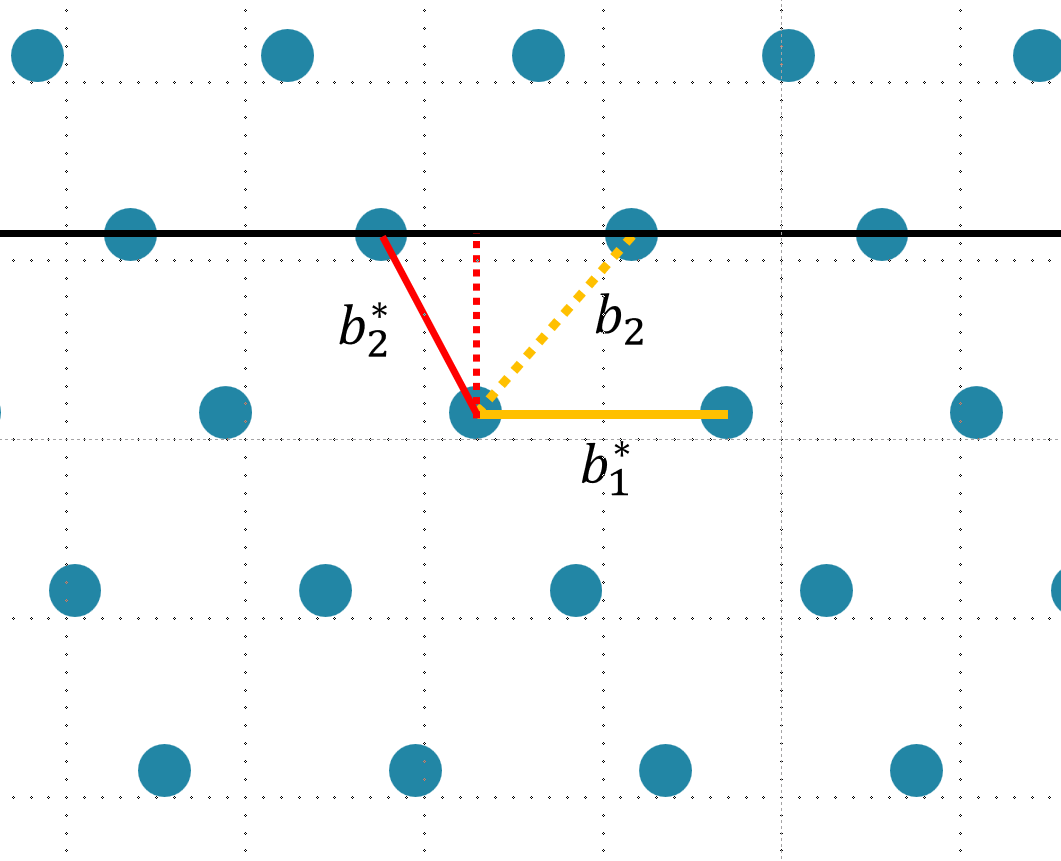
显然这个 $b_2^* = b_2-kb_1^*,k \in(0,1)$，不过由于在格上我们仅可以通过对格基进行一系列系数为整数的线性变换，因此这个 $k$ 我们需要进行一个四舍五入，于是对于上图中所展示的格，我们最终所能得到的尽可能“垂直“的格基为

Gram-Schmidt 正交化的公式为

对于线性无关的向量组 $a_1,a_2,\cdots,a_m$ 令

$b_1 = a_1$

$b_2 = a_2-\frac{(a_2,b_1)}{(b_1,b_1)}b_1$

$b_3 = a_3-\frac{(a_3,b_1)}{(b_1,b_1)}b_1-\frac{(a_3,b_2)}{(b_2,b_2)}b_2$

$\cdots$

$b_m = a_m-\frac{(a_m,b_1)}{(b_1,b_1)}b_1-\frac{(a_m,b_2)}{(b_2,b_2)}b_2-\cdots-\frac{(a_m,b_{m-1})}{(b_{m-1},b_{m-1})}b_{m-1}$

则向量组 $b_1,b_2,\cdots,b_m$ 是正交向量组，且两向量组等价。

那么相较而言，格中的 Gram-Schmidt 正交化就是四舍五入一下系数（大概吧，我猜的），得到一组相对比较“正交”的格基。

这里只是非常非常非常简陋的介绍了一下，想要深入了解的读者还是建议去查阅相关专业书籍。

小结

在这篇文章中我们首先介绍了一下格中常见的难题 SVP 和 CVP，然后展示了一下这两个难题之间的相关性，即 CVP 问题是如何转化为 SVP 问题的。接着提供了一个解决这些难题方案，就是找到正交基，即我们需要进行格基规约。最后我们介绍了一种线性代数中的规约方法——Gram-Schmidt正交化。在下一节中我准备介绍一下在比赛中我们常用的格基规约方法，即 LLL 算法，还有 BKZ 算法。但其实这部分内容对于大多数人来说并没有必要掌握，只需要知道怎么进行调包就可以了。（我就是想单纯记录一下，纯当学习笔记了）

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com