关于微信公众号

这次比赛没啥人打，随便看了看题，但是看了一题就把心态看崩了，还是一道都被六十多人做出来的题，已经这么菜了么，呜呜呜。

cube

解题前的阿巴阿巴

这哪里是密码题，分明就是数学题。让你给出六对(x,y,z)，满足$\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y} = 6$，（欺负人数学不好吗日，感受到深深恶意）

自己做肯定是不会做的，这里找到这个问题的相关页面了

介绍的做法是这样的。首先这条式子可以转化为$x^3 + y^3 + z^3 - 5 * x^2 * (y + z) - 5 * y^2 * (z + x) - 5 * z^2 * (x + y) - 9 * x * y * z = 0$

可以发现是一条三次曲线，然后通过变量替换（对x，y，z进行线性组合映射为X，Y，Z，也可以看作换坐标系）将这条三次曲线映射为一条椭圆曲线。

上述页面的问题是$\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y} = 4$，但没事，我们把这个问题搞懂应该就可以举一反三了。

他用的线性变换是这样子的$(X,Y,Z)^T=\begin{bmatrix} -\frac{95}{2} & -\frac{95}{2} & \frac{277}{12} \newline -\frac{91}{2} & \frac{91}{2} & 0 \newline -6 & -6 & 1 \newline\end{bmatrix} (x,y,z)^T$

可以验证$X^3-\frac{11209}{48}X Z^2+\frac{1185157}{864}Z^3-Y^2 Z=8281(x^3 + y^3 + z^3 - 3x^2(y+z) - 3y^2(z+x) - 3z^2(x+y) - 5xyz)$

这样子问题就转变为求$x^3-\frac{11209}{48}x z^2+\frac{1185157}{864}z^3-y^2 z=0$

这里我们再固定$z=1$，式子就简化为$x^3-\frac{11209}{48}x+\frac{1185157}{864}-y^2=0$，就是一条Weierstrass equations了。

这样我们就可以把数对(x,y,z)映射为这条椭圆曲线上的一个点了，然后文章给出了一个结论，如果映射后的有理点落在下图的红色区域，那么这个数对的三个数就都是正数了。

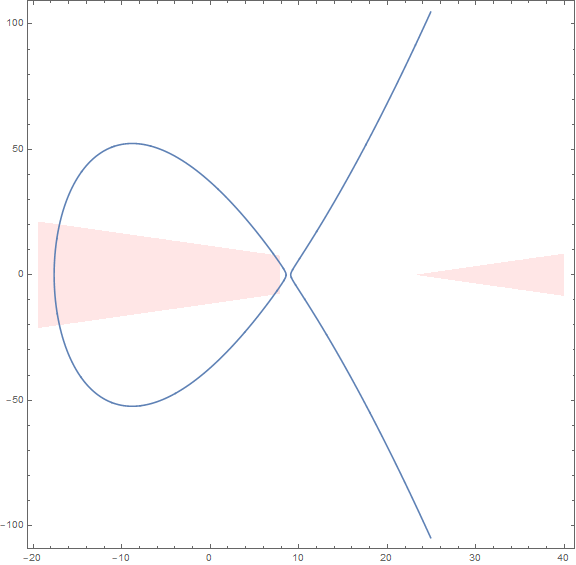
文章说It is easy to verify（有感受到深深的恶意）这个有理点要落在$x\in(\frac{-39 \sqrt{65}-109}{24},\frac{-84 \sqrt{3}-59}{12})\cup(\frac{84 \sqrt{3}-59}{12},\frac{95}{12})$这个区域，我们的数对就都是正整数了。

然后由于在椭圆曲线上有点加法，所以思路就是：

我们可以先获得一个满足方程的初始点，然后通过不断地对这个点进行运算，使其落入到这个区域中，再把区域内的点反映射成数对(x,y,z)，那么我们就解决这个问题了。

但是，但是，但是，最重要的是，这篇文章没有给出这个线性变换矩阵的获得方式（让我去推？不如让我去死）

后来啊，coin给俺来了一个描述这个问题的网页，我在评论区找到了这个，运行平台是Magma

// 
// For my colleagues in Shell with a lot of love,  (and  with a lot of time now since no commuting, cause COVID) 
// Code is commented to explain how to solve the meme  (https://preview.redd.it/p92108lekoq11.jpg?width=367&format=pjpg&auto=webp&s=e0c84917c3d7e130cad06f9ab5a85634b0c88cfb) 
// 
// x/(y+z) + y/(x+z) + z/(x+y) = 4 
// 
// This is the smallest solution: 
// x=4373612677928697257861252602371390152816537558161613618621437993378423467772036 
// y=36875131794129999827197811565225474825492979968971970996283137471637224634055579 
// z=154476802108746166441951315019919837485664325669565431700026634898253202035277999 
// 
// Paste in the site below to execute this code see this result, also read the comments here to understand.  
// The last part of the prints() after executed shows you the solution above. 
// http://magma.maths.usyd.edu.au/calc/ 
// Eduardo Ruiz Duarte  
// toorandom@gmail.com 
// 
 
 
// First we define our environment for our "problem" 
 
R<x,y,z> := RationalFunctionField(Rationals(),3); 
 
problem := ((x/(y+z) + y/(x+z) + z/(x+y)) - 4) ; 
// first note that we know a point after some computation (-1,4,11) that 
// works but has a negative coordinate, the following function returns 0, which means that  
// (x/(y+z) + y/(x+z) + z/(x+y)) - 4 = 0    (just put the -4 in the other side) 
Evaluate(problem,[-1,4,11]); 
 
// after the previous returned 0 , we know the point fits, we continue. 
 
// we multiply by all the denominators of "problem" to get a polynomials 
problem*Denominator(problem); 
// we obtain a polynomial without denominators x^3 - 3*x^2*y - 3*x^2*z - 3*x*y^2 - 5*x*y*z - 3*x*z^2 + y^3 - 3*y^2*z - 3*y*z^2 + z^3 
// We see is cubic, three variables, and every  term has the same degree (3) , therefore this is a cubic  
// homogeneous curve,  we know there is a point which is not the solution we want 
// the point (-1,4,11) fits in the original "problem" so it should fit in this new curve without denominators too (since no denominator becomes 0) 
 
// We transform this equation to a "curve" in Projecive space of dimension 2 
P2<x,y,z> := ProjectiveSpace(Rationals(),2); 
C := Curve(P2,x^3 - 3*x^2*y - 3*x^2*z - 3*x*y^2 - 5*x*y*z - 3*x*z^2 + y^3 - 3*y^2*z - 3*y*z^2 + z^3); 
 
// fit the point to the curve C (no error is returned) 
Pt := C![-1,4,11]; 
 
// Since all cubic homogeneous curve with at least one point define an elliptc curve, we can transform  
// this curve C to an elliptc curve form and just like in cryptography, we will add this known point (mapped to the corresponded curve) 
// with itself until we get only positive coordinates and go back to C (original Problem) 
 
// Below, E is the curve, f is the map that maps   Points f:C -> E  (C is our original curve without denominators, both curves C,E are equivalent  
// but in E we can "Add points" to get another point of E. 
// and with f^-1 we can return to the point of C which is our original solution 
 
E,f := EllipticCurve(C); 
 
//g is the inverse g:E->C  , f:C->E     so g(f([-1,4,11]))=[-1,4,11] 
g := f^-1; 
 
// We try adding the known point Pt=[-1,4,11] mapped to E, 2..100 times 
// to see if when mapped back the added point to C gives positive coordinates 
//, this is 2*Pt, 3*Pt, ...., 100*Pt  and then mapping back to C all these. 
for n:= 1 to 100 do 
 
// we calculate n times the point of C, known [-1,4,11] but mapped (via f) inside E (where we can do the "n times")  
    nPt_inE:=n*f(Pt); 
 
// we take this point on E back to C via f^-1  (which we renamed as g) 
    nPt_inC:=g(nPt_inE); 
 
//We obtain each coordinate of this point to see if is our positive solution, 
// here MAGMA scales automatically the point such as Z is one always 1,  
// so it puts the same denominators in X,Y, so numerators of X,Y are our  
//solutions and denominator our Z,  think of  P=(a/c,b/c,1)   then c*P=(a,b,c) 
    X := Numerator(nPt_inC[1]); 
    Y := Numerator(nPt_inC[2]); 
    Z := Denominator(nPt_inC[1]); 
 
printf "X=%o\nY=%o\nZ=%o\n",X,Y,Z; 
 
// We check the condition for our original problem. 
  if ((X gt 0) and (Y gt 0)) then 
       printf("GOT IT!!! x=apple, y=banana, z=pineapple, check the above solution\n"); 
     break; 
  else 
     printf "Nee, some coordinate was negative above, I keep in the loop\n\n"; 
  end if; 
 
end for;    
 
// We check the solution fits in the original problem 
if Evaluate(problem, [X,Y,Z]) eq 0 then 
    printf "I evaluated the point to the original problem and yes, it worked!\n"; 
else 
    printf "Mmm this cannot happen!\n"; 
end if;

注释就不删了，这样我也不用解释了，主要看到这两行

C := Curve(P2,x^3 - 3*x^2*y - 3*x^2*z - 3*x*y^2 - 5*x*y*z - 3*x*z^2 + y^3 - 3*y^2*z - 3*y*z^2 + z^3);

E,f := EllipticCurve(C);

这两行很关键啊，他把三次曲线映射到椭圆曲线后，还返回了f,这个f就是这个映射关系啊，那么这个问题就解决了啊。

解题过程

首先我们生成一个满足要求的初始点，直接爆破就完事

from fractions import Fraction as Frac
from math import gcd
n = 100
for x in range(-n, n + 1):
    for y in range(-n, n + 1):
        for z in range(0, n + 1):
            if gcd(x, gcd(y, z)) == 1:
                if x**3 + y**3 + z**3 - 5 * x**2 * (y + z) - 5 * y**2 * (
                        z + x) - 5 * z**2 * (x + y) - 9 * x * y * z == 0:
                    print((x, y, z))

(-23, -7, 3)
(-8, -7, 5)
(-7, -23, 3)
(-7, -8, 5)
(-5, 7, 8)
(-5, 8, 7)
(-3, 7, 23)
(-3, 23, 7)
(-1, -1, 1)
(-1, 0, 1)
(-1, 1, 0)
(-1, 1, 1)
(0, -1, 1)
(1, -1, 0)
(1, -1, 1)
(7, -5, 8)
(7, -3, 23)
(8, -5, 7)
(23, -3, 7)

可以得到下面这么多点，但是有用的就俩(-23, -7, 3)、(-8, -7, 5)，其他要么不行，要么都是基于这俩的变形，导致结果只是数对里的值换个顺序。

然后我们去Magam跑这个代码

###Test
//R<x,y,z> := RationalFunctionField(Rationals(),3); 
//problem := ((x/(y+z) + y/(x+z) + z/(x+y)) - 6) ; 
//Evaluate(problem,[-23, -7, 3]); 
 

P2<x,y,z> := ProjectiveSpace(Rationals(),2); 
C := Curve(P2,x^3 - 5*x^2*y - 5*x^2*z - 5*x*y^2 - 9*x*y*z - 5*x*z^2 + y^3 - 5*y^2*z - 5*y*z^2 + z^3); 
Pt := C![-23, -7, 3]; 
E,f := EllipticCurve(C); 
g := f^-1; 
for n:= 1 to 100 do  
    nPt_inE:=n*f(Pt); 
    nPt_inC:=g(nPt_inE); 
    X := Numerator(nPt_inC[1]); 
    Y := Numerator(nPt_inC[2]); 
    Z := Denominator(nPt_inC[1]); 
    
  if ((X gt 0) and (Y gt 0)) then 
       printf("GOT IT!!! x=apple, y=banana, z=pineapple, check the above solution\n");
       printf "n=%o\nX=%o\nY=%o\nZ=%o\n",n,X,Y,Z; 
  end if; 
 
end for;

###Test

//if Evaluate(problem, [X,Y,Z]) eq 0 then 
    //printf "I evaluated the point to the original problem and yes, it worked!\n"; 
//else 
    //printf "Mmm this cannot happen!\n"; 
//end if;

这里最多迭代一百次，能够找到三个答案，因为我们有两个初始点，所以每个找三个，一共就六个了。或者也可以用一个初始点去迭代，就是越到后面的数就越大。

完了最后交互有个坑，就是因为数字太大了，手动交互数据接受的时候可能会被截断，这里得用一手pwntools。

说在最后

这题看着怎么也不像是能有个五六十队伍能做出来的啊。后来雪殇姐姐发来了一个链接，心态崩了，

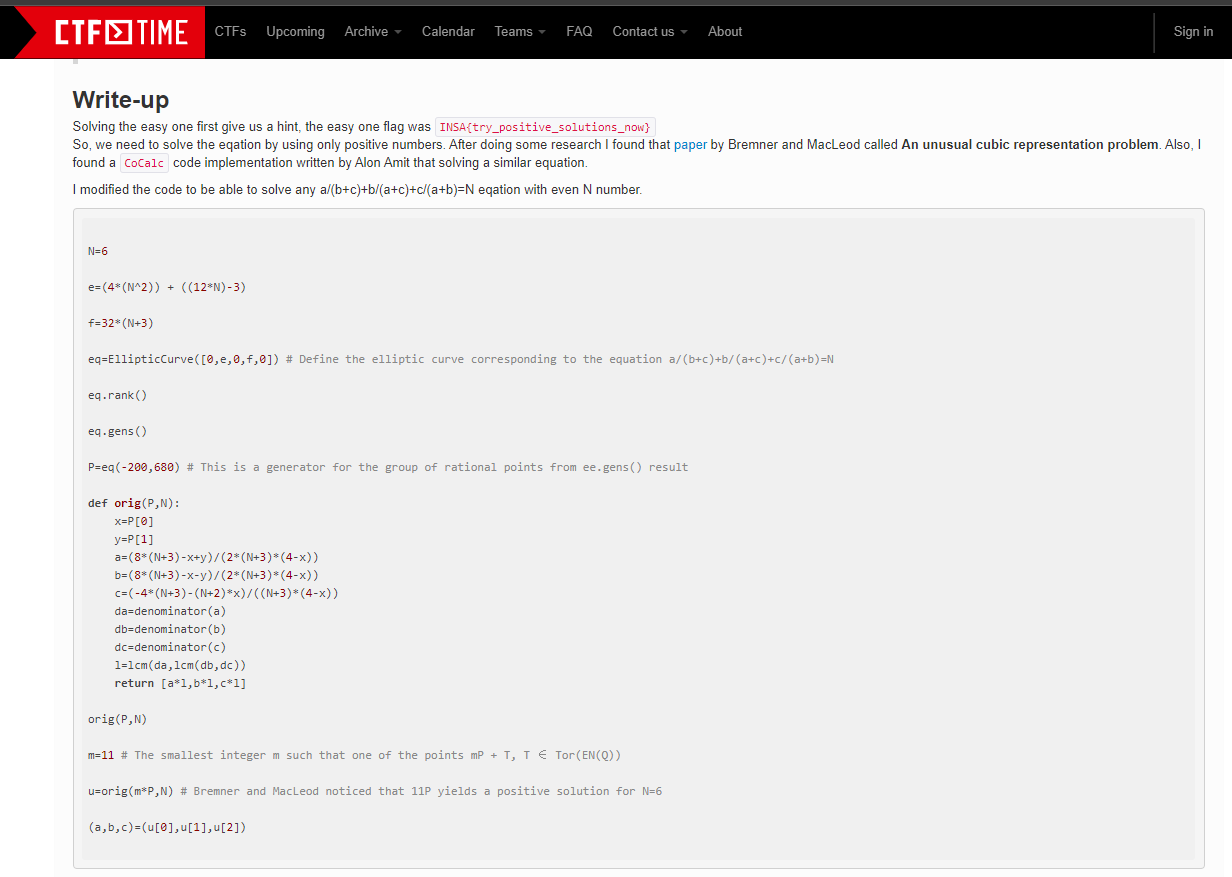
？？？？？我丢你妈的，原题，就尼玛离谱，合着我看了半天，，，，啥也不是，草。

这个做法估计也差不多，但是用的线好像不一样，所以映射关系也不一样，

应该是找到的这个资料里头评论区描述，这条线：$E’_n \colon y^2 = x \bigl(x^2 + (4n(n+3)-3)x + 32(n+3)\bigr)$

映射关系应该是：

$x = 4(n+3)(a+b+2c)/(c-(n+2)(a+b))$

$y = (8n^2+44n+60)(a-b)/(c-(n+2)(a+b))$

但怎么映射回去就不会了，手撸么？看评论区说这个映射关系 Magma 可以搞出来，估计 Magma也能搞回去，但俺也不会啊，有大佬教教么？不过这个脚本也给出关系了，

$a = \frac{8(N+3)-x+y}{2(N+3)(4-x)}$

$b = \frac{8(N+3)-x-y}{2(N+3)(4-x)}$

$c = \frac{-4(N+3)-(N+2)x}{(N+3)(4-X)}$

比赛完心态崩了，出去跑了两公里降了降血压。

re

这道题比赛的时候已经没心情看了，晚上结束后才看的，好像也不是很难。

主要就是一个查找子串的算法。flag就是给出的一个字符串的子串，先出去了，晚上回来更叭可能。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com