密码学学习笔记 之 线性分析入门篇——EzSPN
首发于安全客
前言
上一篇了解了一下差分分析,这次我们结合一道CTF题目聊一聊线性分析
同属于选择明文的差分分析不同,线性分析属于已知明文攻击方法,它通过寻找明文和密文之间的一个“有效”的线性逼近表达式,将分组密码与随机置换区分开来,并再此基础上进行密钥恢复攻击。
在正式介绍线性分析之前,我们还是要介绍一下相关的基础概念,参考《分组密码的攻击方法与实例分析》一书
基础概念
首先还是给出和差分分析一样的一个迭代分组密码的加密流程
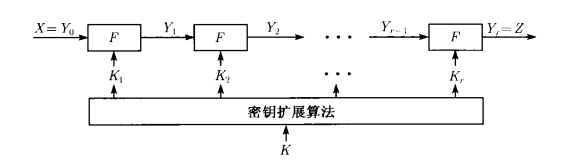
迭代分组密码的加密流程
假设所讨论的迭代分组密码为
$E:{0,1}^n × {0,1}^l \rightarrow {0,1}^n$,
其中 $n$ 为分组长度, $l$ 为密钥长度,任给 $k \in {0,1}^l, E(\cdot,k)$ 是 ${0,1}^n$ 上的置换,加密函数 $E_k(\cdot)$ 由子密钥 $k_i$ 控制的轮函数 $F(\cdot,k_i) = F _ {k _ i}(\cdot)$ 迭代 $r$ 次生成,即
$E_ k(x)=F _ {k _ r} \circ F _ { k _ {r-1}} \circ \cdots \circ F _ {k _ {2}} \circ F _ {k _ {1}(x)}$
其中,轮密钥 $k_i,i=1,2,\cdots,r,$ 由密钥拓展算法对种子密钥 $k$ 进行拓展生成,为方便起见,假设第 $i$ 轮输入和输出分别为 $Y_{i-1}$ 和 $Y_i$,即 $Y_i = F_ {k _i}(Y _ {i-1})$;若明文为$X$ ,则第一轮输入为 $Y_0 = X$;若该分组密码算法有 $r$ 轮,且设密文为 $Z$,则 $Z = Y_r$
内积
设 $a,b \in {0,1}^n, a = (a_1,a_2,\dots, a_n),b = (b_1,b_2,\dots,b_n),$ 向量 a 与 b 的内积定义为 $a \cdot b = \oplus a_i \cdot b_i ,i \in [1,n]$, 其中 $a_i \cdot b_i$ 表示比特 $a_i$ 与 $b_i$ 的与运算,即二元域$\mathbb{F}_2$ 上的乘法运算,$\oplus$ 表示异或运算,即二元域$\mathbb{F}_2$ 上的加法运算
线性掩码
(这是一个比较重要的概念)
设$X \in {0,1}^n$,$X$ 的线性掩码定义为某个向量$\Gamma X \in {0,1}^n, \Gamma X $ 和 $X$ 的内积代表 $X$ 的某些分量的线性组合,即 $\Gamma X \cdot X = {\oplus X_i | \Gamma X_i = 1} $
可以举个简单的例子,比如$X = (0,1,1,0,0,1,1,0)$,$\Gamma X = 6 = 0b110={0,0,0,0,0,1,1,0}$,所以$\Gamma X \cdot X $ 就代表着 $X$ 的第六,第七两个元素的值相互异或,也就是$\Gamma X \cdot X = X_5 \oplus X_6 = 1\oplus 1 = 0$
线性逼近表达式
设迭代分组密码的轮函数为$F(x,k)$,给定一对线性掩码 $(\alpha,\beta)$,称$\alpha \cdot x \oplus \beta \cdot F(x,k)$ 为 $F(x,k)$ 的线性逼近表达式,同样,称$a \cdot x \oplus \beta \cdot E(x,k)$ 为分组密码 $E(x,k)$ 的线性逼近表达式。
假设$p(\alpha,\beta) = Prob_{X,K}{ \alpha \cdot X = \beta \cdot F(x,k)},$ 则 $p$ 表示线性逼近表达式 $\alpha \cdot X \oplus \beta \cdot F(X,K) = 0$ 的概率,在线性密码分析中,一般采用偏差、相关性和势的概念来描述逼近表达式的概率特性,依次定义为
$\epsilon _ F(\alpha,\beta) = p(\alpha,\beta)-\frac{1}{2}$
$Cor _ F(\alpha,\beta) = 2p(\alpha,\beta)-1$
$Pot _ F(\alpha,\beta) = (p(\alpha,\beta)-\frac{1}{2})^2$
将掩码$(\alpha,\beta)$所对应的线性逼近表达式的线性概率定义为 $LP(\alpha,\beta) = (2 \cdot Prob_{X,K}{ \alpha \cdot X = \beta \cdot F(x,k)}-1)^2$
研究线性表达式的概率特性可以简单地描述为研究一对线性掩码的概率特性,即输入掩码 $\alpha$ 到 输出掩码 $\beta$ 的概率传播特性。
线性壳
迭代分组密码的一条 $i$ 轮线性壳是指一对掩码$(\beta_0,\beta_i)$,其中$\beta_0$ 是输入掩码,$\beta_i$ 是输出掩码。
线性特征
迭代分组密码的一条$i$ 轮线性特征$\Omega = (\beta_0,\beta_i,\cdots , \beta_i)$ 是指当掩码为$\beta_0$ 在 $i$ 轮加密的过程中,中间状态$Y_j$ 的掩码为$\beta_j$,其中 $1 \le j \le i.$
线性特征和线性壳的区别在于,线性壳仅仅给定了输入掩码和输入掩码,中间状态的掩码值未指定;而线性特征不仅给定了输入输出掩码,还指定了中间状态的掩码值。
线性壳的线性概率
迭代分组密码的一条 $i$ 轮线性壳$(\beta_0,\beta_i)$的线性概率 $LP(\alpha,\beta)$ 也可记为 $LP(\alpha \rightarrow \beta)$,是指在输入 $X$, 轮密钥 $K_1,K_2,\cdots,K_i$ 取值独立且均匀分布的情形下,当输入掩码为$\beta_0$ ,在经过$i$ 轮加密后,输出掩码为$\beta_i$ 的线性概率。
线性特征的线性概率
类比于线性壳的线性概率,当输入掩码为$\beta_0$,在加密过程中,中间状态$Y_j$ 的掩码取值为$\beta_j$ 的线性概率,其中 $1 \le j \le i$。
好的,有了如上的前置知识,我们来讲讲我们如何用线性分析来区别随机置换$\mathcal{R}$ 和分组密码。
线性区分器
先给出一个命题,对${0,1}^n $上的随机置换$\mathcal{R}$,任意给定掩码$\alpha,\beta,\alpha \neq 0,\beta \neq0,$ 则 $LP(\alpha,\beta ) = 0,$ 即 偏差$\epsilon(\alpha,\beta) = 0$
如果我们找到了一条 $r-1$ 轮线性逼近表达式 $(\alpha,\beta)$,其线性概率$LP(\alpha,\beta) \neq 0$,即偏差$\epsilon(\alpha,\beta) \neq 0$。则利用该线性逼近表达式可以将 $r-1$ 轮的加密算法与随即置换区分开来,利用该线性区分器就可以对分组密码进行密钥恢复攻击。假设攻击 $r$ 轮加密算法,为获得第 $r$ 轮 的轮密钥的攻击步骤如下。
步骤1
寻找一个 $r - 1$轮的线性逼近表达式$(\alpha,\beta)$,设其偏差为$\epsilon$,使得 $|\epsilon(\alpha,\beta)|$ 较大。
步骤2
根据区分器的输出,攻击者确定要恢复的第 $r$ 轮轮密钥 $k_r$(或者其部分比特):设攻击的密钥比特长度为 $l$,对每个可能的候选密钥$gk_i, 0 \le i \le 2^l -1$,设置相应的 $2^l$ 个计数器 $\lambda_i$,并初始化。
步骤3
均匀随机地选取明文 $X$,在同一个未知密钥 $k$ 下加密,(一般是让拥有密钥地服务端帮你加密)获得相应地密文 $Z$, 这里选择明文地数目为 $m \approx c \cdot \frac{1}{\epsilon ^2}$,$c$ 为某个常数。
步骤4
对一个密文$Z$,我们用自己猜测地第 $r$ 轮轮密钥 $gk_i$(或其部分比特)对其进行第 $r$ 轮解密得到$Y_{r-1}$,然后我们计算线性逼近表达式 $\alpha x \cdot X \oplus \beta \cdot Y_{r-1}$ 是否为0,若成立,则给相应计数器$\lambda_i$ 加 1
步骤5
将 $2^l$ 个计数器中$|\frac{\lambda_i}{m} - \frac{1}{2}|$ 最大地指所对应地密钥 $gk_i$(或其部分比特)作为攻击获得地正确密钥值。
Remark 针对步骤1中,我们如何去寻找一个高概率地 $r -1 $ 轮线性逼近表达式呢?例如针对一个S盒,我们可以选择穷举所有的输入、并获得相应的输出,然后穷举输入掩码、输出掩码,去获取这个S盒的相关线性特性。
下面就根据一道CTF中出现的赛题来解释分析上述过程。
实例-[NPUCTF2020]EzSPN
task.py
1 | import os |
题目提供一个交互,能够加密你的输入并返回密文。所以这里是否可以采用差分分析的攻击方法呢,但这里我们讨论的线性分析,所以我们就用线性分析来做这道题目里。
那么看到这里所用加密系统的流程。
关键函数是encrypt_block(pt, ks),
首先是一个明文和一半的密钥异或,然后是进入S盒(题目每次随机生成并提供S盒具体内容),然后trans一下,再进入一个逆S盒,最后再和另一半的密钥异或。
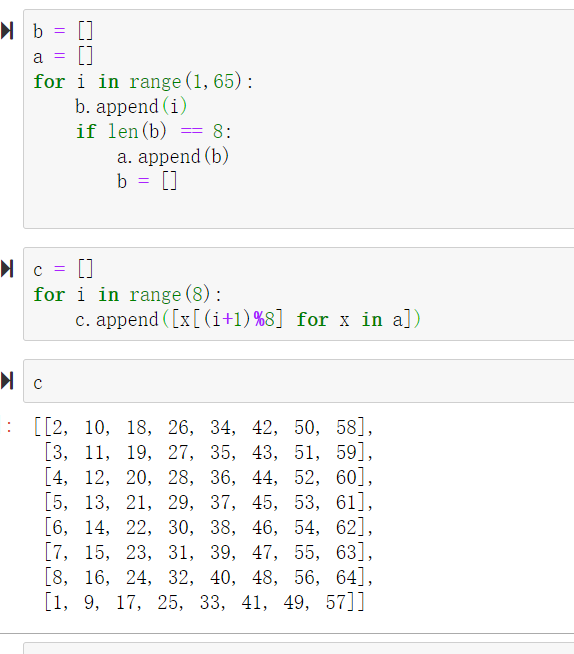
看到这个trans函数,这里有一个int(‘’.join([x[(i+1) % 8] for x in bits]),2),这个(i+1%8)有点类似位移的效果,然后是乘以了一个系数,但这个系数已经定死了,所以没有什么关系。
首先测一个这个trans函数的一个位移效果,大概类似这样
然后整个流程图(画的丑了点)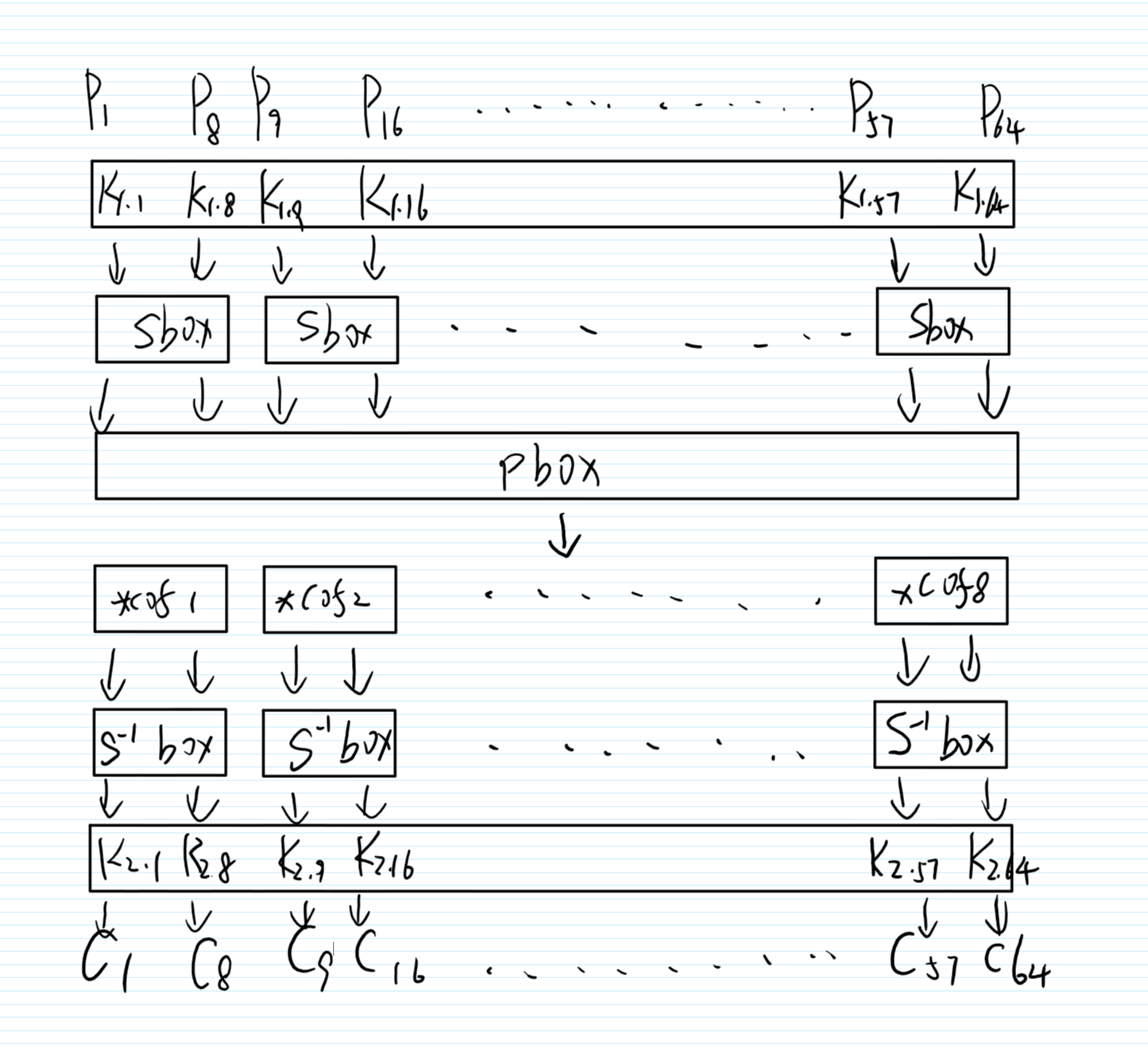
那么针对这道题,我们利用线性分析攻击手法,
首先步骤1,我们去分析S盒的线性特性以找到使得线性表达式偏差大的掩码对$(\alpha,\beta)$。我们穷举所有的S盒的可能的输入并计算出相应的输出,然后穷举所有的输入、输出掩码的组合,然后根据其是否符合满足线性逼近表达式 $\alpha \cdot X \oplus \beta \cdot F(X,K) = 0$ 来更新计数器,最后我们计算相应的偏差表offset
1 | def linearSbox(): |
其中j是输入掩码,k是输出掩码。
这里的offset以输入掩码为行,输出掩码为列,所以这里的cur是获取同一输出掩码下不同输入掩码的偏差
并且在linearInput中记录下同一输入掩码下使得线性表达式偏差最大的输出掩码。
这里我们简单看一下输出的offset表
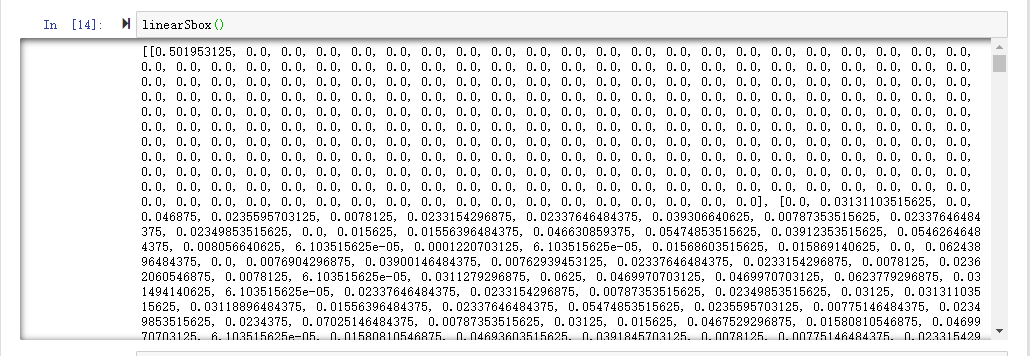
可以看到列表的第一行很特殊,除了第一个是0.5这个极大的值以外,其他都是0。因为在输入掩码为0、输出掩码也为0的话,肯定是能够满足的情况下,针对所有的输入、输出肯定是都能满足线性逼近表达式的,所以偏差达到了最大,0.5。但是换做其他输出掩码的话,针对所有的输出,其最后的表达式的结果分布得很均匀,所以偏差为0。
再举第二行第一列的0.03131…这个值的含义:就是针对所有的256个输入,当输入掩码为1,输出掩码为1时的线性逼近表达式的偏差。即有 256 * (0.03+0.5) ≈ 135 个输入满足(或者不满足)这个线性逼近表达式。
有了S盒的线性特性之后,步骤2是设置一个计数器conter,然后我们开始进入步骤3搜集明文密文对。就随机选择明文,发送给服务端,然后接收服务端返回的密文即可。
接着开始步骤4,由于这里有两轮加密,然后我们在步骤1已经生成了关于单个S盒的一个offset表,这个就相当于是 $1$ 轮线性特征了,那么我们接下来就按照线性分析的攻击思路,
这里我们按字节猜测密钥,首先拿一个密文的第一个字节,异或第一个字节的密钥(枚举)后从S逆盒出去,然后把系数cof除掉,再根据P盒,把这个值换到相应的位置,然后这里我们根据S盒的线性特征选取合适的输出、输入掩码对我们的这对输入进行测试。若满足线性逼近表达式,则True计数加一,否则False计数加一。
最后步骤5,针对每个字节我们都测一万对,取结果偏差最大的key值。这样就完成了密钥每个字节的猜测。
结合代码再细细讲一遍
1 | def calcOffset(pt, ct, j, guessed_key): # 猜测第j段子密钥 |
linearAttack()中我们主要关注那个循环。这里调用了calcOffset函数,传入了一对明文密文对(plain[j], cipher[j])、索引(i)、以及猜测的密钥(guessed_key)。
在calcOffset中,首先用密文异或了guessed_key,然后根据值获取从Sbox的输入,然后乘以了coef(这里已经是原来coef的逆了),接着是u2 = bitxor(ct[j], 0b10000000),用了0b10000000作为掩码,即选取了密文的第一个bit。然后选取 linearInput[1 << ((6 - j) % 8)] 做为明文第一个字节的掩码。
为什么只选明文的第一个字节,以及其掩码的选取这里可能看的不是很直观,因为这里其实包含了两部分。
我们需要回去注意到P盒。当这里j=0,即爆破第一个字节的密钥时,我们选取的是密文的第1个字节,掩码选的是第1个bit,那么这是从P盒输入的哪个bit传来的呢,从P盒我们可以看到这是P盒输入的第一个字节的第2bit传来的,那么P盒输入的第2bit,实际上就是S盒输出的第2bit,也就是S盒的输出掩码为0b01000000,也就是1 << 6。而这个 linearInput 存的就是输出掩码为某个值的使得线性逼近表达式偏差最大的输入掩码。
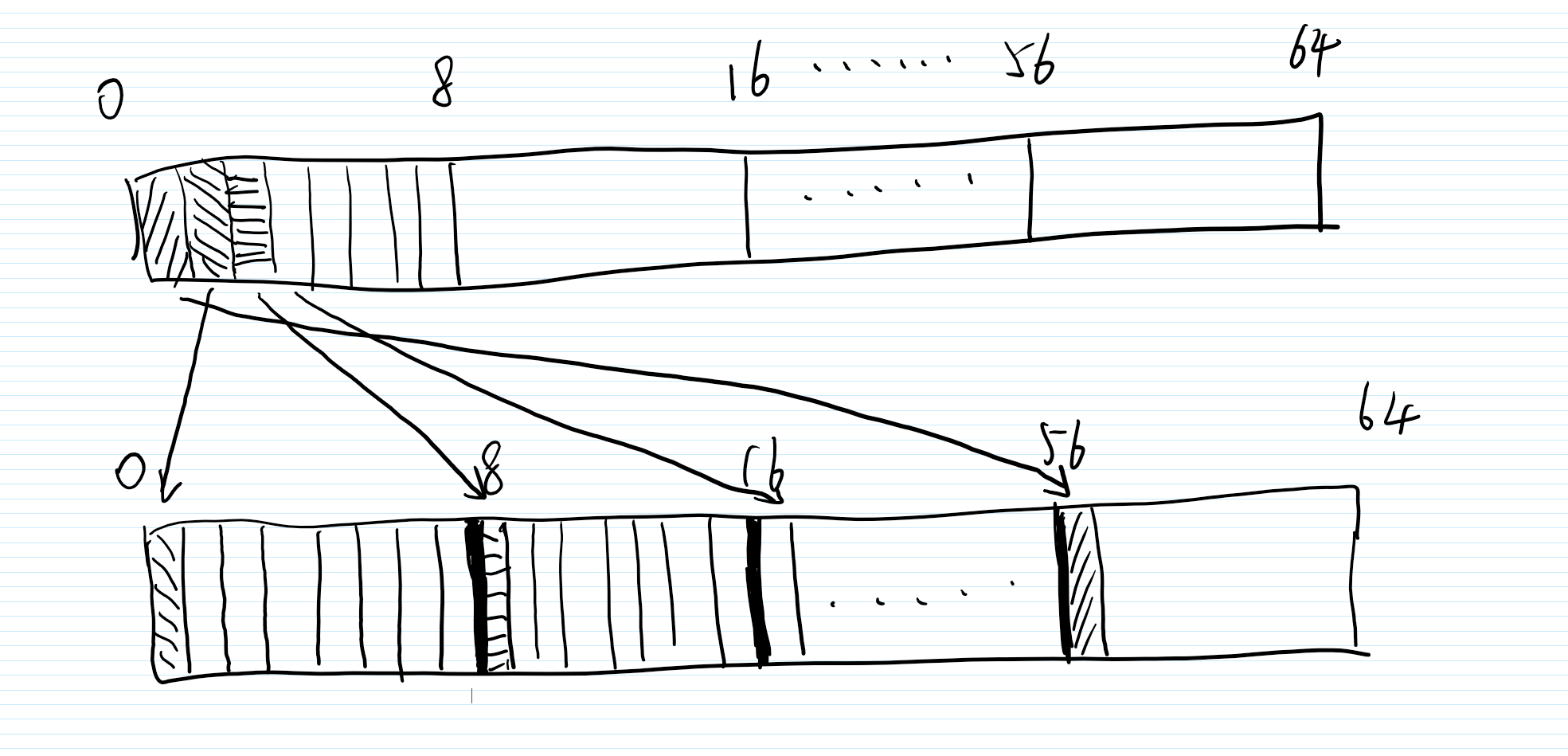
当我们选取密文第二个字节的时候,根据P盒,第二个字节第1个bit来自于明文第一个字节第3个bit,也就是0b00100000,也就是1 << 5,同理可推
所以这里只用选明文的第一个字节,密文不同字节的第一个比特,且输入掩码为 linearInput[1 << ((6 - j) % 8)]。
另外可能还有一个问题,S盒的输入不是明文啊,应该是明文异或了第一个段密钥。确实,但是试想一下,在线性逼近表达式的这个式子中,密钥部分相互异或后,最后无非就是0或者1,而且由于密钥固定,所以针对固定的输入掩码,这个值是固定的。对于返回结果没有影响或者只是一个取反的效果。而我们是根据偏移来判断的,所以正并不影响结果,key的具体的值在这里也就没什么影响。
举个例子,如果输入掩码是0b00110011,输入掩码是0b00001111,那么由于密钥的存在,线性逼近表达式就是这么写:$X_2 \oplus X_3 \oplus X_6\oplus X_7 \oplus K_2 \oplus K_3\oplus K_6\oplus K_7 = Y_4\oplus Y_5 \oplus Y_6 \oplus Y_7$
其中$K_2 \oplus K_3\oplus K_6\oplus K_7$ 这部分无非就是等于 0 或者 1,对于结果没有影响或者只是一个取反的效果,对偏差则没有影响。
爆破出第二部分key的每一个字节之后,我们就可以逆算法流程。由于S盒是双射的,用明文、密文、第二部分key就可以去恢复第一部分的key,然后再写一个解密函数就可以解决这道问题了,
来自出题人的exp:
1 | import os, sys |
那么对于这道简单的两轮分组密码的线性分析就到此告一段落了,但对于分组密码的学习不会到此为止,因为,还有高阶差分、截断差分、不可能差分……
参考资料
- 《分组密码的攻击方法与实例分析》(李超,孙兵,李瑞林) SS=12567685
- https://0xdktb.top/2020/04/19/WriteUp-NPUCTF-Crypto/EzSPN.pdf
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081,也可以邮件至 643713081@qq.com
文章标题:密码学学习笔记 之 线性分析入门篇——EzSPN
文章字数:4.9k
本文作者:Van1sh
发布时间:2021-08-06, 09:24:25
最后更新:2021-08-19, 21:12:17
原始链接:http://jayxv.github.io/2021/08/06/密码学学习笔记之线性分析入门篇——EzSPN/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

