关于微信公众号

​

​ 其实密码学基础系列一直是很想做的一个系列，一方面想要帮助密码学新人或者是想要学习密码学的选手更好的入手密码学，另一方面，作为一个基础薄弱，大学工数、线代、概率论差点挂科的“密码学选手”来说，学到后面愈发的感觉到了基础理论的重要性，于是也想借此夯实一下自己的基础。同时也希望已经入门的密码学选手们不要只把注意力放在高层建筑上，理论基础，真的也很重要。

​ 不过之前一直不知道从何起手。古典密码？但是大家但凡接触过密码学都会知道，古典密码好像跟玩具似的，要么就是脑洞（我们在这里不做这么头脑风暴的事，一切尽可能做到有理有据）。后来在一次次给学员培训，给新手们解答一些简单问题的时候发现，当我在上面侃侃而谈 “ RSA 的加密方式是 密文C 在模 N 下与 明文 M 的公钥也就是 E 次方同余 ” 的时候，学员却在心里面疑惑：一个字符串是怎么变成一个数字然后进行运算的呢？

​ 于是，决定我们故事就从进制与编码开始说起……

进制

​ 听到进制，也许很多读者心里会想：进制？进制转换么？二进制转十六进制是吧，我初中就学过了，8421，abcd，很简单的。就算初高中没有接触过，如果是工科专业，需要学习编程，那么进制也是排在课本中比较前面的章节，这也足以体现进制的重要性。那么我们今天介绍的进制，和上面讲的二进制、十六进制有什么区别呢？我的回答是，没有区别。

​ 这里的进制还真就是那个进制转化的进制，但是我们在学习进制的时候，除了死记硬背进制转化的公式，或者是直接简单粗暴的调用程序内建的函数，我们是否有想过其内在逻辑？除了二进制、八进制、十进制、十六进制，是否还有其他进制？其他进制又有什么用，其他进制和十进制又怎么相互转化？希望这篇文章接下来的内容能够给到读者们一点启发。

​ 那么我们知道，为了计算机的方便，我们有了 01010 这样的二进制，

​ 还是为了计算的方便，一个字节八个比特，对半开来 4 个比特，$2^4 = 16$，于是有了十六进制

​ 但是作为人类，我们还是喜欢纯粹的阿拉伯数字，所以我们还是喜欢用十进制。

​ 那么二进制是怎么转化为十进制的呢？例如 100110，书上告诉我们说有，从右到左，分别为 1，2，4，8，16，32，我们把 “1” 所在的位置对应的数拿过来相加就可以了，于是这里就是 2+4+32 = 38

​ 然后十六进制是怎么转化为十进制的呢？例如 6a4d，一样的，从右到左，分别为 1，16，256，4096，我们有 $d + 4 * 16 + a * 256 + 6 * 4096 = 27213$

​ 于是我们不难总结出一个任意进制到十进制数的转化规则，假设我们现在有一个数 $N$ 是 $x$ 进制记为$N_x=abcde$ ，为了（后面）方便，我们用向量来表示这个数 $N_x = (a,b,c,d,e)$，于是 $x$ 进制转化为十 （$d$ ）进制的规则可以表示成一个函数： $N_d = f_x(a,b,c,d) = a \cdot x^4+b\cdot x^3+c\cdot x^2+d\cdot x_e$

​ 举个🌰，现在我们设 $x =30$，$N_x=(29,11,5,4)$，那么 $N_d=f_{30}(29,11,5,4) = 29 \cdot 30^3+11 \cdot 30^2+5\cdot 30+4=793054$

​ 用向量表示一个数显得很奇怪，但是向量中超过 9 的元素我们又不能用数字表示。于是十六进制引入了字母 $a,b,c,d,e,f$ 来表示 $10,11,12,13,14,15$。那么理论上我们最多可以有36进制，额外再引入字母 $a,b,c,\dots,z$ 来表示。那么，当 $x=256$ 呢？字母已经不够了。一个可行的方案是，我们用两个十六进制字符来表示一个数，$16*16=256$，这样就正好了。

​ 第二颗🌰，现在我们设 $x=256$，有 $N_x=(102,108,97,63,1)$，其中的每一个元素我们用两个十六进制字符来表示，即 $N_x=(66,6c,61,67,01)$，然后拼接 $N_x=666c616701$。转化为十进制就是 $N_d = 102\cdot 256^4+108 \cdot 256^3+97 \cdot 256^2 + 63 \cdot 256 + 1=439904986881$，不过由于256进制下的一个元素又是有两个16进制字符表示的，所以其实整个 $N_x$ 也可以看作是 16 进制数，以第一个元素为例， $ 102 \cdot 256^4 =102 \cdot (16^2)^4 = (6\cdot 16 + 6)\cdot (16^2)^4=6 \cdot 16^9 + 6 \cdot 16^8$，于是 $N_d$ 也可以记为 $N_d = 6 \cdot 16^9+6\cdot 16^8 + 6\cdot 16^7 + \cdots+1 = 439904986881$

编码

​ 前面讲了进制，但是我们还是没有解决学员心中的疑惑：一串消息是怎么变成一个数字的呢？

​ 想要将字符变成一个数字，这就少不了编码了。不论是 base64 编码，还是黄道十二宫，还是大伙会在 CTF 题目中遇到的其他奇奇怪怪的编码，透过现象看本质，编码无非就是一个双射函数，能够将一个字符以某种固定规则转换成另一个字符（或者是图案，or sth else)。双射函数又称为置换，置换密码又可以看作是以表为密钥的编码（于是世界线收束了）。

​ 由于世界各地用着各自不同的语言和字符，那么将字符转化成数字的编码规则也有很多种，我们这里暂且只讨论公认的将英文字母和通用标点符号转化为数字的规则 ASCII 码。

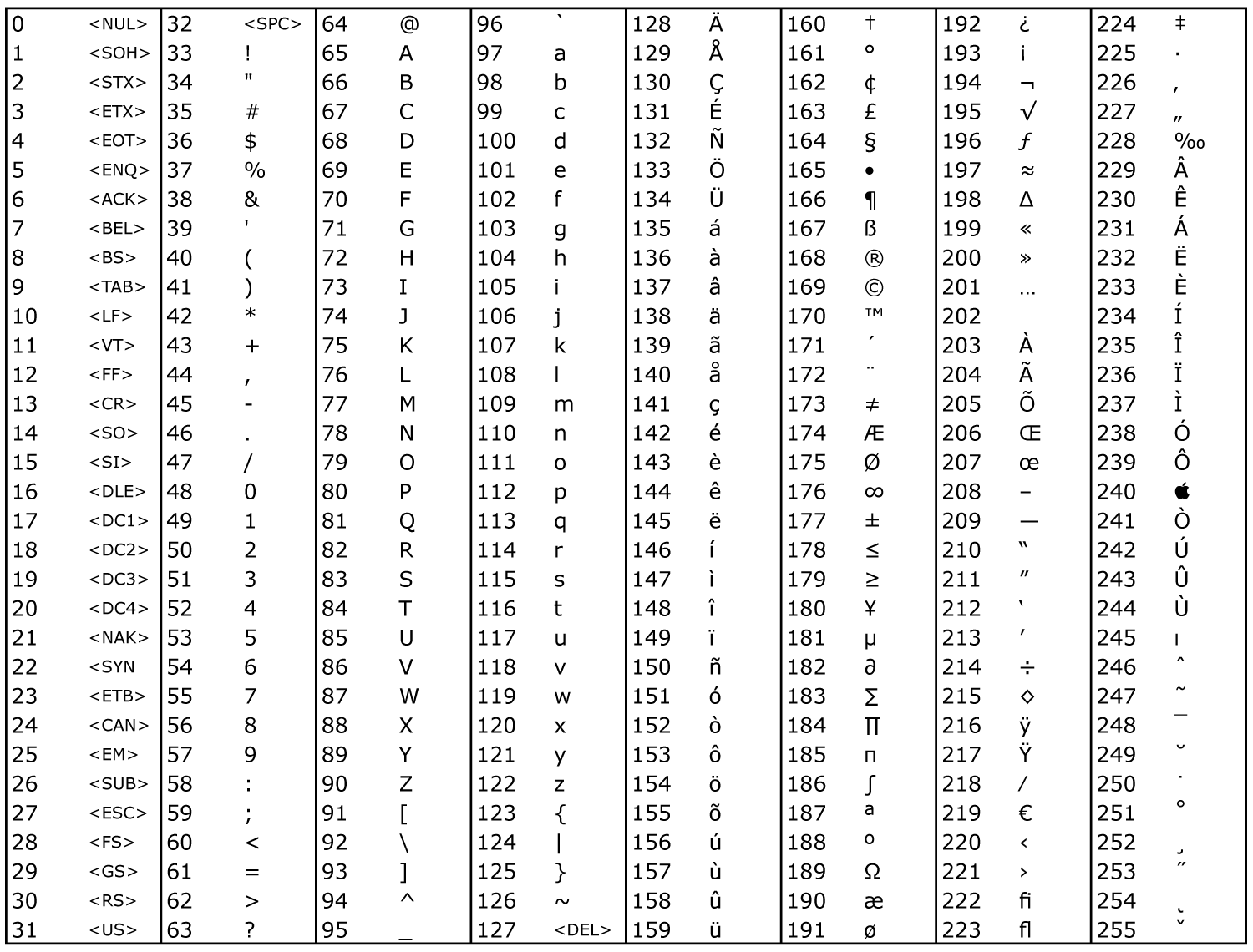
上图是完整的 ASCII 码表，一共 256 个字符（因为一个字节 8 比特，最多能有 $2^8=256$ 种可能），其中可见字符的范围是 33-126 。以 python 程序语言为例，我们可以通过调用内建函数 chr 和 ord 来根据 ASCII 码表规则实现字符和数字的转换。

第三颗🌰

>>> print(ord('f'))
102
>>> print(chr(102))
f

现在我们已经有能力将一个字符转化为数字了，那么对于一个字符串呢？字符串是由字符和字符拼接而来，所以我们也可以很简单的将数字拼接起来，所以 flag 就可以表示为 10210897103。

但是这样有一个问题，字符转化的十进制数有的是两位，有的是三位，这会导致在将数字转化为字符串的时候产生歧义，102108 究竟是 102 和 108 还是 10 、21 和 08。那么我们可以添加一个规则，比如在将数字拼接的时候，不是三位数的数字我们在左边用 0 补齐后再添加，于是 flag 就可以表示为 102108097103。

但是注意到，ASCII码表最大也才 256，一个字符用三位数字去表示其实浪费了很多空间，最高位才只用到 0,1,2。因此我们使用的方案是将数字转化为十六进制再拼接。前面我们也提到256个数刚好可以用两位十六进制字符表示。于是 flag 就可以表示为 666c6167

那么想要将 flag 转化为十进制数字，就是先将其编码为十六进制数 666c6167 ，然后再转化为十进制数 $f_{16}(6,6,6,c,6,1,6,7) = 1718378855$，由于是用两位十六进制数表示一个字符，那么想要更好的体现这样的对应关系，我们也可以将其看作是 256 进制，于是有 flag = $f_{256}(66,6c,61,67)=1718378855$ ，结果是一样的。

现在我们已经能够通过编码和进制将字符串转化为一个数字了，根据上述过程，我们可以构造出如下代码

def bytes_to_long(s): # 字符串转数字
    value = 0 		# 初始化数值为 0 
    s = s[::-1]		# 将字符串逆序，方便从低位，也就是最右边的字符开始计算
    position = 0 	# 初始化位置为 0，从最低位开始 
    for i in s: 	# 遍历每一个字符
        tmp =  ord(i) # 获取字符的 ascii 码
        value += tmp*(256**position) # 根据字符的 ascii 码和所在位置进行赋值并相加
        position += 1	# 下一个字符的位置
    return value

print(bytes_to_long("flag")) 

# 1718378855

那么如何将数字转化为字符串呢？理论上来说就是上述过程的逆过程，先将这个十进制数转化为十六进制，然后以每两个字符为单位进行查表。或者是将这个数转化为 256 进制，然后对每一个值进行查表。

那么，如何将一个数转化为 256 进制呢？具体一点就是如何使得 $1718378855 \to (102,108,97,63)$

更一般的，如何将一个数转化为任意（ $x$ ）进制呢？

这里引入两个运算方法，一个是取余运算 $%$，一个是整除 $//$。这两个运算相信大家都不陌生，这里就不再介绍了其运算规则了。

为了便于理解，我们还是从十进制数开始，假设有数 $N = 123456$，我们计算 $N % 10$ 能够取得个位 6，我们计算 $N//10$ 能够抹去个位 6 得到 12345；

如果是十六进制数，我们设$N = 1d2b = 7467$，我们计算 $N %16$ 也能取得 “个” 位 11 也就是 b，我们计算 $N//16$ 能够抹去个位 b 得到 1d2 ；

于是我们发现，当取余和整除的数刚好为进制的时候，我们就能获得这个数在该进制下的 “个” 位，也就是最低位。

因此，当我们想将一个十进制数转化为 256 进制时，我们先对其取余 256，我们就能获得该数在 256 进制下的最低位。然后整除 256 ，就能抛去原来的最低位，使得原来倒数第二位，变成现在的最低位，然后继续取余，继续整除… 直到这个数整除 256 之后为 0。

第四颗🌰，将 1718378855 转化为 256 进制

>>> 1718378855 % 256
103
>>> 1718378855 // 256
6712417
>>> 6712417 % 256
97
>>> 6712417 // 256
26220
>>> 26220 % 256
108
>>> 26220 // 256
102
>>> 102 % 256
102
>>> 102 // 256
0

于是我们得到 $1718378855 \to (102,108,97,103)$

根据上述过程，我们可以构造出如下代码

def dec_to_base(number,base): # 十进制转任意进制
    res = [] 	# 初始化结果向量
    while number != 0:	# 直到 number 为 0 后停止循环
        res.append(number % base)	# 获取最低位
        number //= base		# 抛去原来最低位
    return res[::-1] # 将结果逆序，使得最低为在最右侧

print(dec_to_base(1718378855,256))

#　[103, 97, 108, 102]

于是将数字转化为字符串只需要先将数字转256进制再加一个查 ascii 表的操作（在 python中就是调用 chr 函数）

def long_to_bytes(number): 	# 字符串转数字
    res = dec_to_base(number,256)
    return ''.join(chr(i) for i in res)		# 将 res 列表中的每一个元素根据 ascii 转为字符后拼接返回

print(long_to_bytes(1718378855))	

# flag

在 CTF 中的密码学赛题中我们常常会遇到已知部分明文的情况，例如明文信息是 flag{+secret+ } ，其中 flag{} 是已知的 6 个字符，secret 是未知字符，假设其长度为 x，那么我们该如何用数字去表示呢？

flag{ 转为十六进制是 666c61677b，}转为十六进制是 7d，那么整个数转为十六进制应该是 666c61677b????????7d 的样子，其中 ? 的个数为 2x。那么为了方便操作我们其实可以将这样一个数划分为已知和未知的部分，分别是666c61677b00000000007d （其中 0 的个数为 2x ）和 secret * 256 ，之所以 secret 要乘以 256 是因为最低位已经被 } 占用了，需要将 secret 整体向左边移，挪一个位置出来。

于是最终将该明文转化为数字的 python 写法： bytes_to_long(“flag{“ + “\x00” * x + “}”) + 256 * secret。其中 x 是 secret 的字符串长度，\x00 是转化成数字后是 0 的字符。

第五颗🌰

沿用上述举例，如果 secret 是字符串 B@se，于是

>>> hex(bytes_to_long('flag{\x00\x00\x00\x00}'))
'0x666c61677b000000007d'
>>> hex(bytes_to_long('B@se'))
            '0x42407365'
>>> hex(bytes_to_long('B@se') * 256)
		  '0x4240736500'
>>> hex(bytes_to_long('flag{\x00\x00\x00\x00}') + bytes_to_long('B@se') * 256)
'0x666c61677b424073657d'
>>> hex(bytes_to_long('flag{B@se}'))
'0x666c61677b424073657d'

没想到一个简单的进制与编码我能叨逼叨这么多，那么最后就留给大家一道和进制相关的 CTF 赛题作为收尾啦。

n = 0xfd483cae510f722d545ccb13f940e8cbc0dfc5b4c75ffdc12b6a14f853d68897fe122501336c787a9d38a99d523bd3e6aa3fd61fdb2432b17527f2d7b98de57e3bc90a1d035daf555325f67402627636bd228afb1a9170c2361d2a1f8e113355fb6fc2717e1188fbe3fbc02999e756827e05c5a7a2be48be7ff5300dafb0b357d3533988df6e6ff32bdcaf21e16e07945a217ce443fa1c501abd3b153e5c5b2e29153000757eecc36eaa89bd6daed77f30e9bd851f75ab7b3605ead6c0c997a3d875f8ea98700e6f42ecc5d827fb14a12f84f0fed2d633130968dfc0c08e294dd2146ae45ad5ee4daa0c6769d9f8755f255f3124e8d67b3d4ec50e4fdc5d7019
e = 65537
c = 16411821211611337214724819464616046484604819498801628453983400297622859204066614768714306394377399946483916492941697806055626837163976693456090461368653000804371891000670205080036735740054550705112060817141377980816092122965568139177603425152082968333619485198797515252985189599285514588084552283828181161664915538303519369723218744692679449760043940760322399347786482803962796338138002092963052927910131740586854377865633969525672611542236857071163982820804701897749463363261518316995466730076224322233282380872363681382468214816524720659164343727144787174800200731589392815404816233029553171705935050928381022518077

题解：后台私信关键词 进制与编码题解，嘻嘻 :）

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com