关于微信公众号

这篇文章中的大部分基础知识都是摘自 《An Introduction to Mathematical Cryptography》中的第七章：Lattices and Cryptography。对其中的内容进行了一些删减和整合，旨在向初学者介绍一些基础的格理论知识。不过仍需要读者掌握一定的线性代数基础知识。

首先是格 （Lattice）的定义：我们设有 $n$ 个 $m$ 维的相互线性独立的向量 $v_1,\dots,v_n \in \mathbb{R}^m$，那么由 $v_1,\dots,v_n$ 生成的格 $L$ 就是这些向量的所有系数为整数的线性组合。
$$
L = {a_1v_1+a_2v_2+\cdots+a_nv_n:a_1,a_2\dots,a_n \in \mathbb{Z} }
$$
对应的，这样一组向量则称为格 $L$ 的基 (basis)。

所以格和向量空间是很像的，不过由于“系数为整数”的要求，使得相对于连续的向量空间，格是由一系列离散的格点组成的。形如下图，格中的格点应该是无限多的，并且任一维度中，相邻格点之间的距离是固定不变的。（下面我们会再具体做说明）

我们再用一个”生动形象“的🌰来说明：

首先我们定义一个坐标系的原点作为参照。

于是我们就可以定义一个一维向量（如果将点与点之间加上箭头的话大家可能会熟悉些）

然后这个一维向量通过一系列“系数为整数”的线性组合（$v,-v,2v,-2v,3v\cdots $），那么它就可以生成一个一维的格

如果此时我们引入一个在这个维度之外的向量

那么同样的，取原来维度中的任一向量和这个向量作为基进行各种线性组合（$v+w,v-w,v+2w,v-2w \cdots$），于是就可以生成一个二维的格

同理，我们还可以生成三维的格，

四维的、五维的等等也都可以（不过显然这不再是我们能够用图像表示出来的了）

相信到这里大家对格应该有一个大致的认识了（很简单的嘛），那么我们继续后面的话题。对于一个格 $L$ 来说，他的基并不是唯一的，任何能够生成格 $L$ 的向量集合 $v$ 都可以称为 $L$ 的格基。显然 $L$ 的任意格基中所包含的向量数量是相等的，而格 $L$ 的维度也正是由格基中向量的数量所决定。那么格基之间是否可以相互转换呢？

我们设 $L$ 的两组格基 ${v_1,\cdots,v_n },{w_1,\cdots,w_n}$。那么由于它们都是 $L$ 的格基，因此其中的每一个向量也都在格上， 即 $v_1,\cdots,v_n ,w_1,\cdots,w_n \in L$，那么显然对于任意的 $w_i,i\in[1,n]$，其都可以由格基 ${v_1,\cdots,v_n }$ 表示，于是有

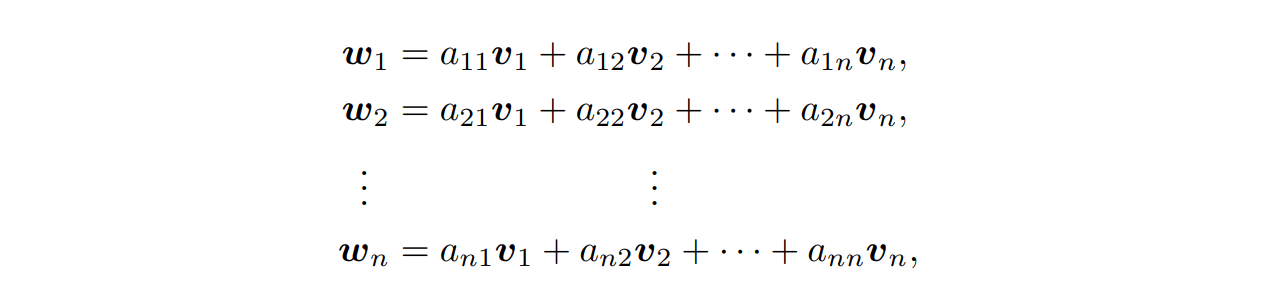
并且由于格的性质，所有的系数 $a_{ij}$ 都是整数。我们将这些系数提取出来，就可以得到一个系数矩阵

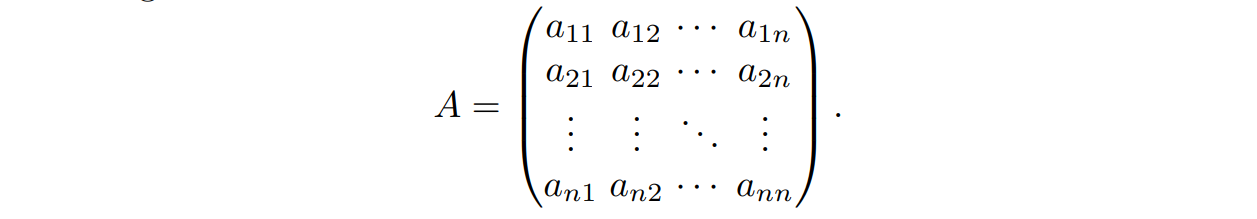
那么式子就可以记为 $w = A \times v$，如果我们想用 $w$ 表示 $v$，那么就是 $v = A^{-1} w$。

注意到由于 $1 = det(I)=det(AA^{-1})=det(A)det(A^{-1})$，而 $A$ 中所有元素均为整数，因此有 $det(A) = \pm 1$。根据线性代数中的知识我们有 $A^{-1}=\frac{A^}{det(A)}$，而伴随矩阵 $A^$ 的计算过程中又不涉及任何的除法，于是 $A^*$ 中的元素都是整数，因而 $A^{-1}$ 中的元素也均为整数。

因此我们得到一个结论，$L$ 的任意两个格基都可以通过一个行列式为 $\pm1$ 的整数矩阵进行相互转换。

第二颗🌰，我们考虑一个三维的格 $L$，其一组格基为 $v_1=(2,1,3),v_2=(1,2,0),v_3=(2,-3,5)$，我们将其写为矩阵的形式

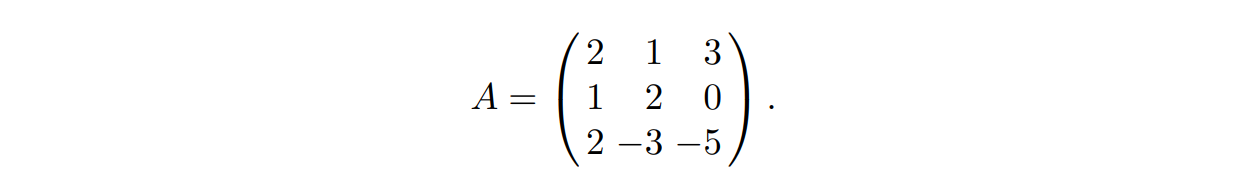
然后我们构造三个也在 $L$ 中的向量：$w_1=v_1+v_3,w_2=v_1-v_2+2v_3,w_3=v_1+2v_2$，我们将这些系数取出来，构成系数矩阵 $U$:

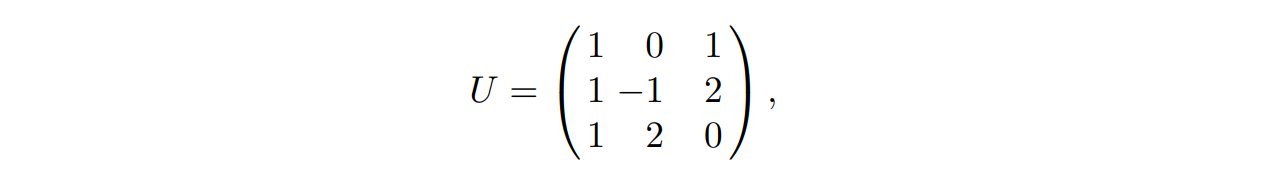
于是由向量 $w_1,w_2,w_3$ 构成的矩阵 $B$ 为：

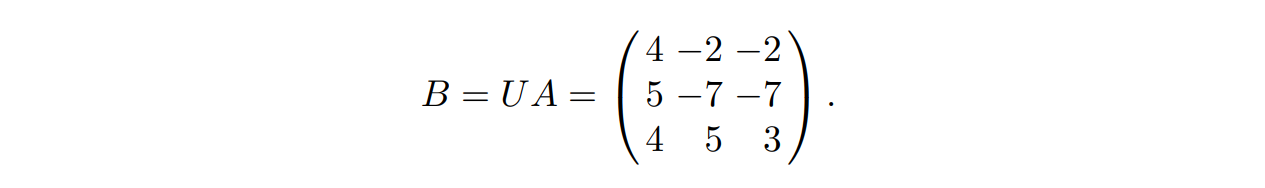
由于矩阵 $U$ 的行列式为 $-1$，因此向量 $w_1,w_2,w_3$ 也是 $L$ 的一组格基，而 $U$ 的逆矩阵为

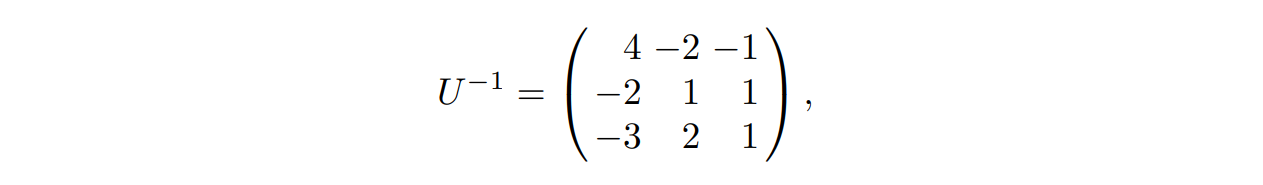
矩阵 $U^{-1}$ 则揭露了如何用 $w$ 表示 $v$：$v_1=4w_1-2w_2-w_3,v_2=-2w_1+w_2+w_3,v_3=-3w_1+2w_2+w3$

了解了上述内容后，我们可以还从另外一个角度定义格：设 $m$ 维的实数空间 $\mathbb{R}^m$ 中的一个子集 $L$，其在加法运算下满足封闭性，于是我们可以称之为 可加子群，如果对于 $L$ 中的任意向量 $v$，存在一个常数 $\epsilon \gt 0$，满足
$$
L \cap{w \in \mathbb{R}^m:||v-w||\lt \epsilon }={v}
$$
则称 $L$ 为 可加离散子群。更形象点说，（以 3 维为例）对于 $L$ 中的任一元素 $v$，在其周围半径为 $\epsilon$ 的空间内都没有其他元素。

定理：当且仅当 $\mathbb{R}^m$ 下的一个子集 $L$ 是可加离散子群，我们称 $L$ 为格。

对于那部分没有格点的空间，我们称之为格 $L$ 的基本域（fundamental domain），记为

$$
\mathcal{F}(v_1,\dots,v_n)={ t_1v_1+t_2v_2 + \cdots + t_nv_n : 0 \le t_i \lt 1}
$$
下图展示了一个二维格的基本域

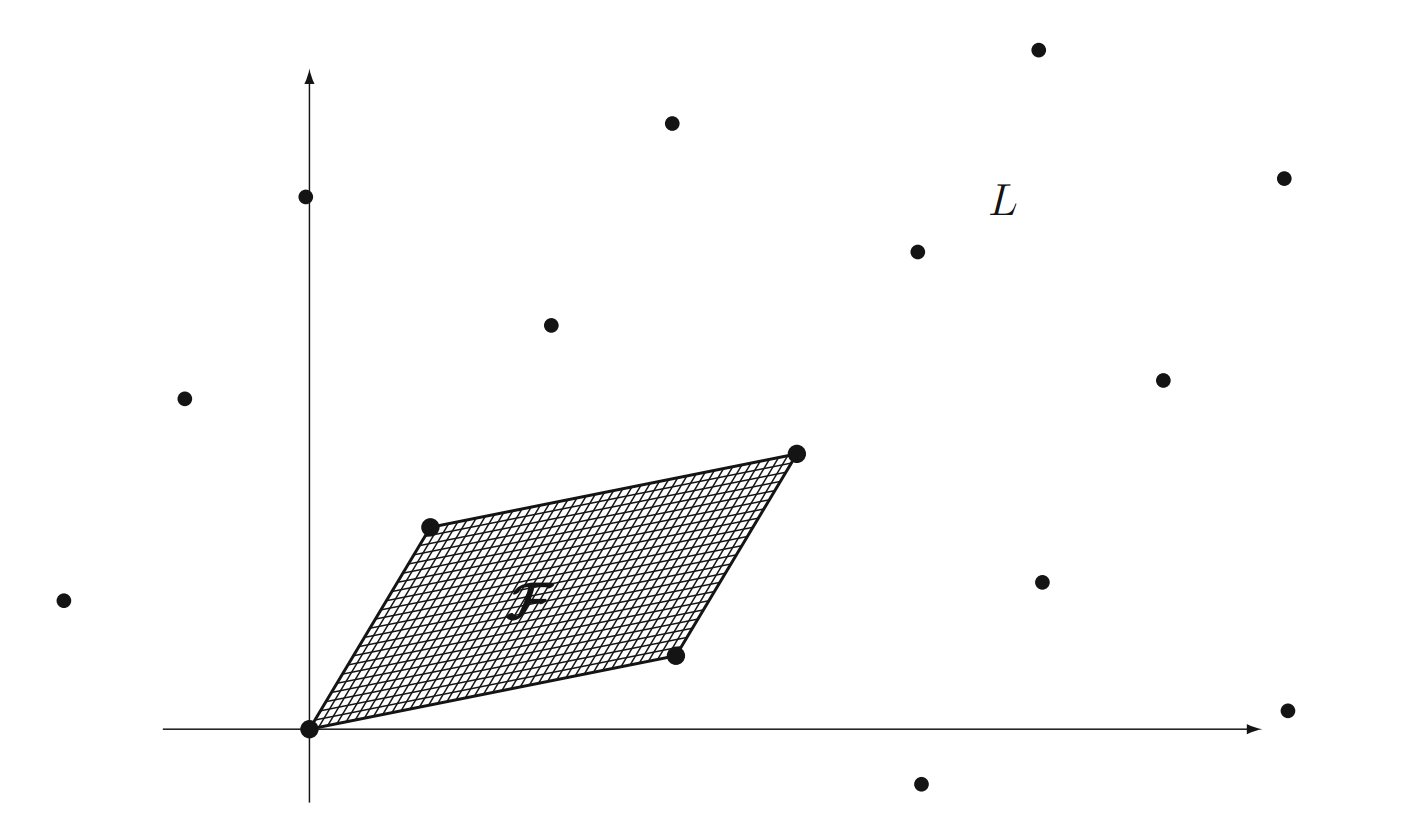
有了基本域的概念，结合 $L$ 中的格点，我们就可以表示实数空间 $\mathbb{R}^n$ 中的任意向量 $w \in \mathbb{R}^n$ 了，记为
$$
w = t+v ,(t\in \mathcal{F}, v\in L)
$$

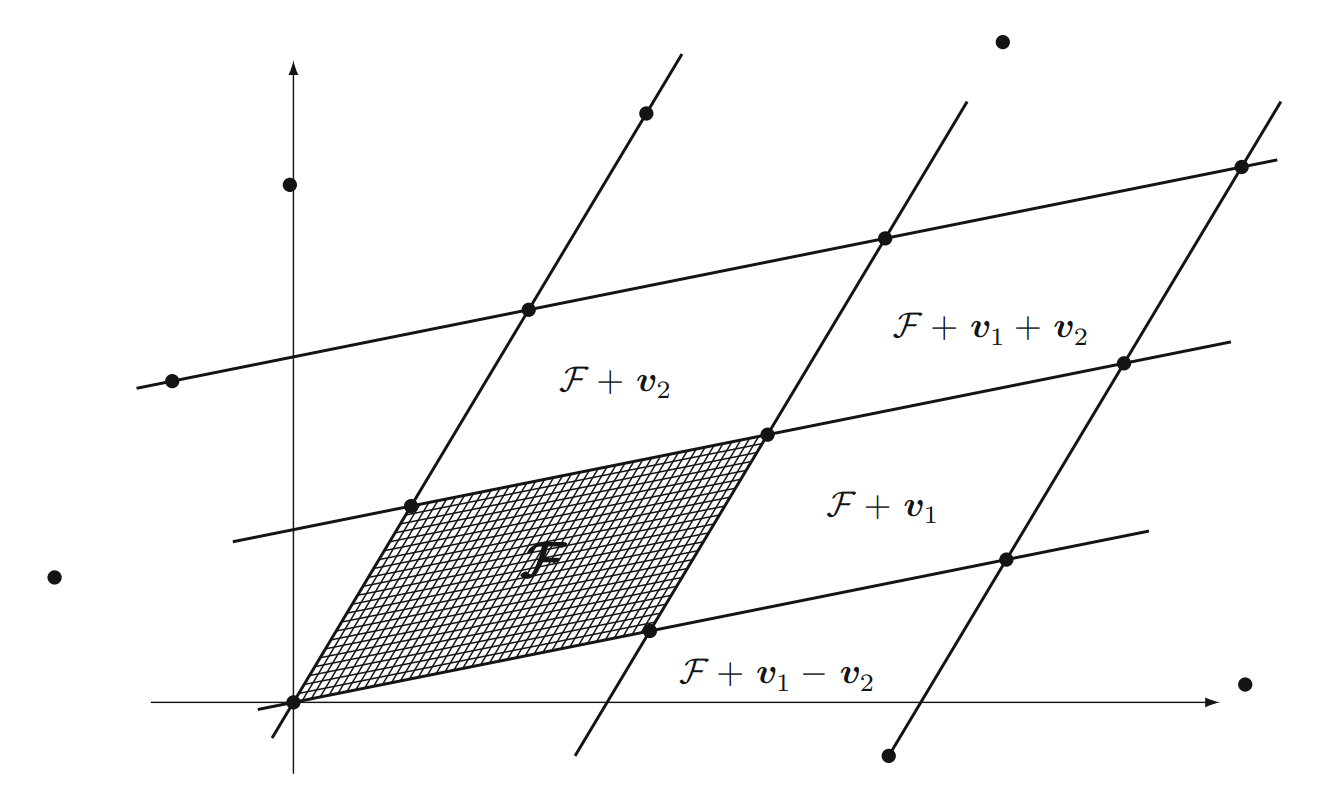
另外，根据图片，结合前面我们对线性代数的学习，我们可以很自然的想到，对于 $n$ 维的格 $L$，设 $\mathcal{F}$ 为 $L$ 的基本域。那么 $\mathcal{F}$ 的度量（volume）就是 $L$ 的行列式 (determinant）记为 $det(L)$。

如果我们把格基的各个向量视为 $\mathcal{F}$ 的各个边，那么在各个向量长度不变的情况下，当且仅当各个向量相互正交时，$\mathcal{F}$ 取得最大值。于是我们引出 Hadamard’s 不等式：
$$
det(L) = Vol(\mathcal{F})\le ||v_1||||v_2||\cdots||v_n||
$$
当各个向量越趋于正交，不等式则越趋于相等。

如果对于 $L$ 的某一格基 $(v_1,\dots,v_n)$，我们记其对应的基本域为 $\mathcal{F} = \mathcal{F}(v_1,\dots,v_n)$，再设 $v_i=(r_{i1},r_{i2)},\dots,r_{in})$，记

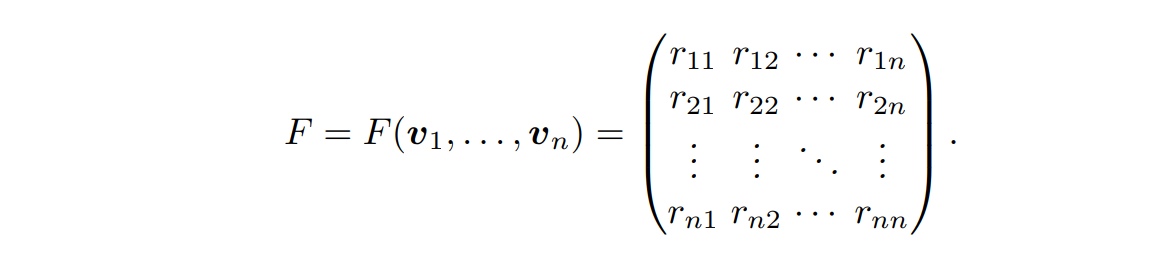
于是我们有
$$
Vol(\mathcal{F}(v_1\dots,v_n))=|det(F(v_1,\dots,v_n))|
$$
而我们在前文提到，$L$ 的不同格基可以通过一个行列式为 $\pm1$ 的整数矩阵进行相互转换，即 $F(v_1,\dots,v_n)=AF(w_1,\dots,w_n),det(A)=\pm1$。于是我们不难得出， $L$ 的任意基本域的度量都相等。形象点来说，就是所有格点周围的空间大小都是相同的。

那么对于格基础理论的介绍就到此为止了，对于感兴趣还想要继续深入了解的读者可以自行查阅相关数学书籍。下一篇文章将介绍一些格中经典的数学问题，以及对应的密码学场景。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com