（我不懂）密码学系列之异或运算

Van1sh 密码小屋 Lattice
创建时间:
字数:3.3k 阅读:
  1. 原理知识
  2. 一次一密（One Time Pad)
  3. 多次一密（Many Times Pad）
    1. 2019 De1CTF XORZ
    2. 2023 SEECTF-non-neutrality
  4. 总结

原理知识

异或运算想必大家刚接触编程语言的时候就有学习到，它是一个二元运算符，符号常用 $\oplus$，在编程语言中常为 ^，运算性质也是非常的简单，我们设两个输入分别为 $A,B$ 输出为 $C$，于是可以得到下表。

A B C
0 0 0
0 1 1
1 0 1
1 1 0

可以看见异或运算与加法类似，唯一不同的是最后一行。于是异或运算也称为 “模二加“，即
$$
A\oplus B = C \iff A+B \equiv C \pmod 2
$$
异或运算还有如下性质：

交换律：$A ⊕ B = B ⊕ A$

结合律：$A ⊕ (B ⊕ C) = (A ⊕ B) ⊕ C$

恒等律：$A ⊕ 0 = A$

自 逆：$A ⊕ A = 0$

这几条性质结合起来使得异或运算具有对合性，即 $f(f(x))=x$，

举个例子，设 $f(x) = x \oplus B$，那么
$$
f(A) =A \oplus B = C
$$

$$
f(f(A)) = (A \oplus B) \oplus B = A
$$

正是因为异或运算的对合性，再加上其在计算机中可以高效运行，于是异或运算成为了现代密码学中对称密码的基石。

我们先来看一个简单的例子，来自 cryptohack

1
2
3
4
KEY1 = a6c8b6733c9b22de7bc0253266a3867df55acde8635e19c73313
KEY2 ^ KEY1 = 37dcb292030faa90d07eec17e3b1c6d8daf94c35d4c9191a5e1e
KEY2 ^ KEY3 = c1545756687e7573db23aa1c3452a098b71a7fbf0fddddde5fc1
FLAG ^ KEY1 ^ KEY3 ^ KEY2 = 04ee9855208a2cd59091d04767ae47963170d1660df7f56f5faf

解题：

我们已知 KYE1 和 KEY2 ^ KEY1，我们对这两个数进行异或操作得到： KYE1 ^ KEY2 ^ KEY1

使用交换律，得到： KYE1 ^ KEY1 ^ KEY2

根据自逆，我们有：0 ^ KEY2

根据恒等律，我们得到了：KEY2

以此类推，我们可以使用 KEY2 和 KEY2 ^ KEY3 得到 KYE3

使用KEY1，KEY2，KEY3 和 FLAG ^ KEY1 ^ KEY3 ^ KEY2 得到 FLAG

当然，比较简单的方法，就是一次性使用 KEY1， KEY2 ^ KEY3 和 FLAG ^ KEY1 ^ KEY3 ^ KEY2 ，

将他们异或在一起就可以直接得到 FLAG。

一次一密（One Time Pad)

然后我们来看看宇宙无敌的具有无条件安全的一次一密。

Vernam 的一次一密于1917年获得专利，是一种极其简单、完全保密的密码系统，尽管效率很低。密钥 $k$ 由一串二进制数字 $k_0,k_1,…,k_N$ 组成 。它用于加密二进制明文字符串 $m_0,m_1,…,m_N$ ，通过将两个字符串逐位异或运算在一起。然后密文 $c=c_0,c_1,…,c_N$ 由下式给出
$$
c_i=k_i\oplus m_i \forall i\in{0,1,\dots,N}
$$
每个密钥只使用一次，然后被丢弃，系统的名称也由此产生。由于每个密钥的使用概率相等，并且只有一个密钥将给定的 $m$ 加密到给定的 $c$，即密钥 $m⊕ c$。可以证明的是 Vernam 的一次一密具有无条件安全性。

举一个简单的例子就是加密者可以使用密钥 $1$ 加密 $1$ 得到密文 $1\oplus 1=0$，但是破解者在没有密钥的情况下无法判断密文 $0$ 是由 $1\oplus 1$ 计算得来的，还是由 $0 \oplus 0$ 得来的。一个比特有 $2$ 种可能性，那么 $n$ 个比特就有 $2^n$ 种可能性。

不过也正是因为效率原因，并且也存在密钥分发问题，一次一密在现实中的应用并没有推广开来。（属于是胎死腹中）

多次一密（Many Times Pad）

既然一次一密效率太低了，那么如果多次重复使用一个较短的密钥可行么？我们先来看下面这个问题

2019 De1CTF XORZ

1
2
3
4
5
6
7
8
9
10
11
12
13
from itertools import *
from data import flag,plain

key=flag.strip("de1ctf{").strip("}")
assert(len(key<38))
salt="WeAreDe1taTeam"
ki=cycle(key)
si=cycle(salt)
cipher = ''.join([hex(ord(p) ^ ord(next(ki)) ^ ord(next(si)))[2:].zfill(2) for p in plain])
print cipher
# output:

# 49380d773440222d1b421b3060380c3f403c3844791b202651306721135b6229294a3c3222357e766b2f15561b35305e3c3b670e49382c295c6c170553577d3a2b791470406318315d753f03637f2b614a4f2e1c4f21027e227a4122757b446037786a7b0e37635024246d60136f7802543e4d36265c3e035a725c6322700d626b345d1d6464283a016f35714d434124281b607d315f66212d671428026a4f4f79657e34153f3467097e4e135f187a21767f02125b375563517a3742597b6c394e78742c4a725069606576777c314429264f6e330d7530453f22537f5e3034560d22146831456b1b72725f30676d0d5c71617d48753e26667e2f7a334c731c22630a242c7140457a42324629064441036c7e646208630e745531436b7c51743a36674c4f352a5575407b767a5c747176016c0676386e403a2b42356a727a04662b4446375f36265f3f124b724c6e346544706277641025063420016629225b43432428036f29341a2338627c47650b264c477c653a67043e6766152a485c7f33617264780656537e5468143f305f4537722352303c3d4379043d69797e6f3922527b24536e310d653d4c33696c635474637d0326516f745e610d773340306621105a7361654e3e392970687c2e335f3015677d4b3a724a4659767c2f5b7c16055a126820306c14315d6b59224a27311f747f336f4d5974321a22507b22705a226c6d446a37375761423a2b5c29247163046d7e47032244377508300751727126326f117f7a38670c2b23203d4f27046a5c5e1532601126292f577776606f0c6d0126474b2a73737a41316362146e581d7c1228717664091c

根据题面我们有 $c_i = p_i \oplus k_i \oplus s_i$

其中由于 $s_i$ 我们是知道的，因此可以得到 $p_i \oplus k_i = c_i \oplus s_i$

于是我们先爆破密钥 $k$ 的长度，想法很简单，我们认定明文 $plain$ 都是由可见字符组成，并且我们的 $k$ 是 flag，显然肯定也都是可见字符（我们假设只有字母数字和下划线）。因此我们先将密文按照某一长度进行分组，假设长度为 3，那么分组结果为

1
2
3
[0,3,6,9...]
[1,4,7,10...]
[2,5,8,11...]

然后对组内每一个元素异或所有的可见字符，将结果中的可见字符放入集合最终取交集。结果不为空的说明长度正确。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from Crypto.Util.number import *
from Crypto.Util.strxor import strxor
from string import printable

keytable = "0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ_"
ci = "..."
s = b"WeAreDe1taTeam"

ci = bytes.fromhex(ci)

# c = p^k = ci^s
c = strxor(ci,(s*((len(ci)//len(s))+1))[:len(ci)])

def bruce_printable(s):
	TMP = set()
	for each in printable:
		tmp = chr(ord(each)^s)
		if tmp in keytable:
			TMP.add(tmp)
	return TMP


for k_len in range(1,38):
	candidates = []
	for j in range(k_len):
		block = [c[k_len*i+j] for i in range(len(c)//k_len)]
		candidate=set()
		init = True
		for eachbyte in block:
			tmp_candidate=bruce_printable(eachbyte)
			if init:
				candidate = tmp_candidate
				init = False
			else:
				candidate &= tmp_candidate
		if candidate:
			candidates.append(candidate)
	#print(candidates)
	if k_len == len(candidates):
		print("[+]",k_len)

运行脚本我们得到 key 的长度为 30，（如果将 key 的范围变大，会得到更多的可能长度）

随后我们对 key 的每一个字节进行爆破，规则与上述方法一样，先分组，然后组内的所有字节与单个密钥异或，如果解密均为可见字符，说明该密钥字符可能正确。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
k_len = 30
key_candidates=[]
for j in range(k_len):
	block = [c[k_len*i+j] for i in range(len(c)//k_len)]
	keyi_candidate = []
	for keyi in keytable:
		for eachbyte in block:
			if chr(ord(keyi)^eachbyte) not in plaintable:
				break
		else:
			keyi_candidate.append(keyi)
	if not keyi_candidate:
		print("[-] error")
		exit()
	key_candidates.append(keyi_candidate)
print(key_candidates)

结果得到非常多的候选集和，于是我们将plain的字符集缩小

1
plaintable="1234567890qwertyuiopasdfghjklxcvbnmQWERTYUIOPSDFGHJKLZXCVBNM\'` ;,."

得到的候选集合就大大缩小了：

1
[['W'], ['3', '4'], ['k', 'l'], ['c'], ['0', '7'], ['j', 'm'], ['3'], ['t'], ['H', 'O'], ['j'], ['h', 'o'], ['1'], ['n'], ['u'], ['5', '9'], ['2', '5'], ['r', 'u'], ['n'], ['1'], ['o'], ['j'], ['O'], ['t'], ['3'], ['m'], ['0', '7'], ['c', 'd'], ['k', 'l'], ['3', '4'], ['W']]

最后根据解密明文再一一尝试我们最终能够得到 flag：W3lc0m3tOjo1nu55un1ojOt3m0cl3W

在上述解题过程中我们发现，如果密文数据越多，明文和密钥的字符集越小，我们就越能够准确的恢复出密钥，并解密得到明文。于是我们思考，如果这里被加密的明文是完全随机的呢？每个字节都有 256 种可能。如此，重复使用密钥还有关系么？

2023 SEECTF-non-neutrality

出题人题解：https://demo.hedgedoc.org/8qpnrgxeTiSKCl4WueGIHA?view

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from secrets import randbits
from Crypto.Util.number import bytes_to_long
import os

flag = os.environ.get('FLAG', 'SEE{not_the_real_flag}').encode()

# get a one-time-pad in which not exactly half the bits are set
def get_xorpad(bitlength):
    xorpad = randbits(bitlength)
    return xorpad if bin(xorpad).count('1') != bitlength // 2 else get_xorpad(bitlength)

def leak_encrypted_flag():
    return bytes_to_long(flag) ^ get_xorpad(len(flag) * 8)

# I managed to leak the encrypted flag a lot of times
if __name__ == '__main__':
    for _ in range(2**16):
        print(leak_encrypted_flag())

题目随机生成一个比特串，与固定的flag字符串进行异或然后输出，总共给了 65536 组数据。乍一看觉得和上面的题目差不多，但这里被加密的是完全随机的比特串，我们无法再以可见字符为标准以进行区分。

但这里的比特串还是有一点限制，在于随机比特串的 1 比特和 0 比特的数量必然是不相等的。我们记比特串 1 比特的数量为其汉明重量，然后测试密文得到比特串长度是 272，因此随机比特串的汉明重量 不为 136。于是我们将所有生成的比特串的汉明重量进行分类：

  1. 汉明重量为奇数：$50%$
  2. 汉明重量等于136（被舍弃）：${272 \choose 136}/2^{272}\approx 4.8%$
  3. 汉明重量为偶数但不等于136：$45.2%$

于是理论上用于加密 flag 的比特串的汉明重量奇偶比为：10：9，

我们检测一下密文的汉明重量奇偶比

1
2
3
4
>>> from collections import Counter
>>> arr = [int(x) for x in open('nn_out.txt').readlines()]
>>> print(Counter(bin(x).count('1')%2 for x in arr))
Counter({1: 34422, 0: 31114})

奇偶比为 10：9，并且我们还能够知道 flag 的汉明重量为偶数。

随后我们定义一个神器的函数 $f(x,y)$，其表示对于 $x$ 比特长的比特串，汉明重量奇偶性与 $y$ 相同但是不等于 $y$ 的可能取值数量。例如我们有 $f(5,3)=6$，因为 5 比特长，且汉明重量为奇数但不为 3，于是汉明重量只能是 1 和 5，于是所有可能为
$$
00001,00010,00100,01000,10000,11111
$$
不难推出的是 $f(x,y)=2^{x-1}-{x \choose y}$ 【奇偶性去掉一半，再去掉汉明重量等于 $y$ 的所有组合】

我们注意到这六个比特串的每一个比特位置，都是 4 个 0 比特和 2 个 1 比特。

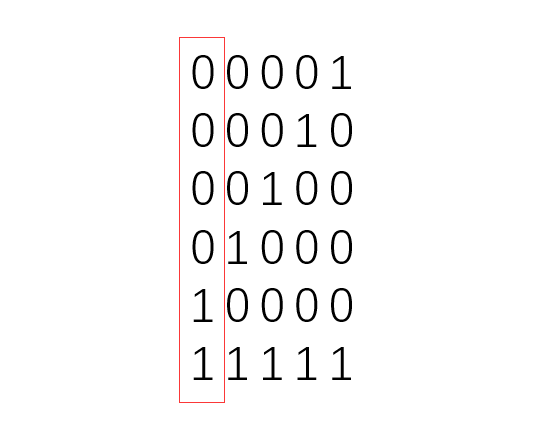
这表示每个位置的取值可能性比为 “0”:”1” = 4 : 2。比较关键的点是这里可以用 $f$ 表示为 $f(4,3):f(4,2)$ 。可以利用组合数的性质（${n\choose m}={n-1\choose m}+{n-1\choose m-1}$）推一下有 $f(x,y)=f(x-1,y)+f(x-1,y-1)$。

于是我们准备解题：根据我们定义的 $f$ 函数，我们需要先把所有汉明重量为奇数的抛掉（这样剩余用于加密的随机比特串的汉明重量均为偶数）

1
2
arr = [x for x in arr if bin(x).count('1')%2 == 0]
arrbits = np.array([[int(a) for a in f'{x:0272b}'] for x in arr])

然后根据我们已知的 flag 的格式 SEE{******************}，将随机比特串的对应位置的比特确定下来。然后我们计算每个位置的比特可能性。

例如第一个符合要求的密文串为

3253110189075583532909324934537273169857320522865536346363834070130933364482802356

flag 能确定的位置分别是 SEE{} 所对应的位置和每一个字节的第一个比特（可见字符第一个比特都是0）总共 69 个比特，即

1
2
3
4
5
6
7
8
9
10
11
flag = 'SEE{?????????????????????????????}'
flagbits = np.array(bits(flag.encode()))

known = np.array([False] * 272)
for i, c in enumerate(flag):
    if c == '?':
        known[8*i] = True
    else:
        known[8*i:8*i+8] = True

print(known)

我们将密文串和已知部分的 flag 串异或，得到的比特串将有效位置记录下来，

1
2
>>> np.count_nonzero(known * (arrbits[0] != flagbits), -1)
35

能够得到其中 35 个 1 比特。于是这个随机比特串剩余部分就不可能有 $136-35=101$ 个 1 比特。总共有 $f(272-69,101)$ 种可能【剩余比特串汉明重量不为 101，但是需要是奇数，因为偶数（比特串总汉明重量）- 奇数（35：比特串总已知汉明重量）是奇数】。于是未知位置的比特为 “1” 或 “0” 对应的可能比为 $f(202,101):f(202,100)$。

这样一组数据就测完了，我们也能够得到 flag 在对应位置的比特值的可能比。

对于每一组我们都这样测下来，然后将 flag 对应位置的比特值可能性 相加*，根据最终可能概率来确定该处为 0 或者 1。

*相加：这里具体如何进行加权并没有一个明确的说法，但又是解题的关键。出题人在这里使用了对数，即每个位置加上 $log(f(x-1,y))-log(f(x-1,y-1))$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from collections import Counter
from pwn import bits, unbits
from scipy.special import binom
import numpy as np

# determine the parity of our flag
arr = [int(x) for x in open('nn_out.txt').readlines()]
print(Counter(bin(x).count('1')%2 for x in arr))
# Counter({1: 34422, 0: 31114})
# This means the flag has an even number of set bits

# set up array with our encrypted bits
arr = [x for x in arr if bin(x).count('1')%2 == 0]
LEN = max(arr).bit_length()
assert LEN == 272
arrbits = np.array([[int(a) for a in f'{x:0272b}'] for x in arr])

# set up array with our guesses for the flag
flag = 'SEE{?????????????????????????????}'
flagbits = np.array(bits(flag.encode()))

# set up array of which positions are known. it's ASCII so every MSBit is set
known = np.array([False] * 272)
for i, c in enumerate(flag):
    if c == '?':
        known[8*i] = True
    else:
        known[8*i:8*i+8] = True

# this is the same function defined above, but in the log space
def f(n,x):
    return np.log(2.0**(n-1) - binom(n,x))


while n := sum(~known):
    # calculate our probabilities! this has a scale of -inf to inf rather than the usual 0 to 1
    k = 136 - np.count_nonzero(known * (arrbits != flagbits), -1)
    probs = (f(n-1, k) - f(n-1, k-1)) @ (2 * arrbits - 1)
    # out of all the unknown bits, get the 10 with the best probability
    inds = np.nonzero(~known)[0]
    inds = inds[np.argsort(-abs(probs[inds]))[:10]]
    # set these flag bits to the corresponding sign 
    flagbits[inds] = probs[inds] > 0
    known[inds] = True
    # print our best estimate of the flag
    print(unbits(np.where(known, flagbits, probs > 0)))

经过测试，发现每次确定10个比特我们能得到一个最接近正确答案的值：b'SEE{__litevally_any_bias_is_bad__}'

而正确的 flag 为：SEE{__literally_any_bias_is_bad__}，仅差了一个比特。

可见，尽管只是对加密原文（随机比特串）有了一点点的限制（汉明重量不为某一个值），在数据量足够大（也就是密钥重复使用的次数足够多）的情况下，我们也能够最大程度的对密钥进行恢复。不过也因为这里的密钥是可见字符，这给我们提供了不小的帮助。

总结

异或真简单。

异或有点东西。

我不懂异或，懂不了一点呜呜呜呜呜。

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com

赏

文章标题:（我不懂）密码学系列之异或运算

文章字数:3.3k

本文作者:Van1sh

发布时间:2023-06-29, 00:00:00

最后更新:2023-08-14, 20:30:51

原始链接:http://jayxv.github.io/2023/06/29/（我不懂）密码学系列之异或运算/

版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

©2020 Van1sh

Built with Hexo and 3-hexo theme

目录
×

喜欢就点赞,疼爱就打赏