密码学学习笔记 之 差分分析入门篇——四轮DES
首发于安全客
前言
密码学学习笔记断更快半年了,最近又重新拾起了对密码学的学习,以一篇对四轮DES的差分分析“复出”。
对于差分密码分析的学习,参考《分组密码的攻击方法与实例分析》
这里就不重新介绍一遍DES的算法流程了,网上一大把。我们研究对DES算法的分析时,由于DES的初始置换及其逆置换均以公开,故在安全性分析时就可以将其忽略。另外我们这里暂且只分析四轮DES,所以有很多概率相关的概念也可以暂时不用涉及。
DES差分分析的关键就在于其S盒差分分布的不均匀特性,何为不均匀特性,即相同的差分进入S盒,输出的差分是不均匀分布的。
不过在详细介绍之前,还是先声明一些概念比较好。
基础概念
迭代分组密码的加密流程
假设所讨论的迭代分组密码为
$E:{0,1}^n × {0,1}^l \rightarrow {0,1}^n$,
其中 $n$ 为分组长度, $l$ 为密钥长度,任给 $k \in {0,1}^l, E(\cdot,k)$ 是 ${0,1}^n$ 上的置换,加密函数 $E_k(\cdot)$ 由子密钥 $k_i$ 控制的轮函数 $F(\cdot,k_i) = F _ {k _ i}(\cdot)$ 迭代 $r$ 次生成,即
$E_ k(x)=F _ {k _ r} \circ F _ { k _ {r-1}} \circ \cdots \circ F _ {k _ {2}} \circ F _ {k _ {1}(x)}$
其中,轮密钥 $k_i,i=1,2,\cdots,r,$ 由密钥拓展算法对种子密钥 $k$ 进行拓展生成,为方便起见,假设第 $i$ 轮输入和输出分别为 $Y_{i-1}$ 和 $Y_i$,即 $Y_i = F_ {k _i}(Y _ {i-1})$;若明文为$X$ ,则第一轮输入为 $Y_0 = X$;若该分组密码算法有 $r$ 轮,且设密文为 $Z$,则 $Z = Y_r$
差分值
设 $X,X^* \in {0,1}^n,$ 则 $X$ 和 $X ^ $ 的差分值定义为 $\Delta X = X \oplus X^$
差分对
设 $\alpha , \beta \in {0,1}^n,$ 假设迭代分组密码的输入对$(X,X^)$ 的差分值为 $X \oplus X^ = \alpha$,经过 $i$ 轮加密之后,输出对 $(Y_i,Y_i^) $ 的差分值为 $Y_i \oplus Y_i^ = \beta$,则称$(\alpha,\beta)$ 为该分组密码的一个 $i$ 轮差分对,特别地,当 $i=1$ 时,$(\alpha , \beta)$显示了论函数 $F$ 的差分传播特性,称 $\alpha$ 为 $F$ 的输入差分,$\beta$ 为 $F$ 的输出差分。
由于这里我们暂且之分析四轮DES,故上述概念就已足够。
首先我们先分析输入差分经过论函数 $F$ 的基本组件后输出差分的性质:
- 密钥加:$(x \oplus k) \oplus(x^* \oplus k) = x \oplus x^*$
- 拓展变换 $E$:$E(x \oplus k)\oplus E(x^* \oplus k) = E(x \oplus k \oplus x^* \oplus k) = E(x \oplus x^*)$
- $S$ 盒:$S(x) \oplus S(x^) = y \oplus y^$,结果不确定,不仅与$x \oplus x^*$ 有关,还与 $x$ 有关
- $P$ 置换:$P(y) \oplus P(y^) = P(y\oplus y^)$
我们可以看到,基本组件中除 $S$ 盒外,其他线性组件的差分传播都是确定的,只有 $S$ 盒这个非线性组件使得差分传播存在不确定性。而一般来说,只有通过不确定性才能获得信息量,因此,对论函数的差分分析在本质上是根据 $S$ 盒的差分传播特性来恢复密钥。
因此,为恢复轮函数 $F$ 中进入第 $i$ 个 $S$ 盒的密钥,我们选择明文对 $(x,x^)$,使得进入第 $i$ 个 $S$ 盒的输入差分非零。然后我们需要获得此次轮函数的输出差分$\Delta = F(x\oplus k)\oplus F(x^ \oplus k)$,根据 $P$ 置换的可逆性,求得 $\delta = P^{-1}(\Delta)$,由$(E(x),E(x^*),\delta)$ 可建立第 $i$ 个 $S$ 盒的差分分析模型。(注:这里的$E(x),E(x^*)$ 为拓展变换 $E$)
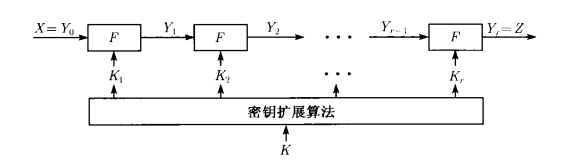
4轮 DES 算法的差分分析
流程图如下
我们记:
- 明文对和相应的差分记为$(P,P^*)$ 和 $P’$
- 密文对和相应的差分记为$(T,T^*)$ 和 $T’$
- 明文左半部分、右半部分及其差分记为$(L,R)$ 和 $(L’,R’)$
- 密文左半部分、右半部分及其差分记为$(l,r)$ 和 $(l’,r’)$
- 第1、2、3、4轮函数的输入和输入差分依次记为$a,b,c,d$ 和 $a’, b’,c’,d’$
- 第1、2、3、4轮函数的输出和输出差分依次记为$A,B,C,D$ 和 $A’, B’,C’,D’$
4轮DES的差分分析本质上仍然是对S和的差分分析,
首先我们由密文对 $T = (l,r),T^* = (l^,r^),$可以获得第4轮轮函数的输入对$(r,r^)$,进而也可以获得8个 $S$ 盒的输入对(密钥加之前的数据)为 $(E(r),E(r^));$ 简单分析 $S$ 盒针对差分的扩散特性以及拓展变换 $E$ 的性质可知,第 4 轮轮函数的输入差分 $r’$ 也即 $d’$ 经过拓展变换 $E$ 后(成为 $S$ 盒的输入差分),$E(r’)$ 几乎会让 8 个 $S$ 盒 都活跃,即这个 8 个 $S$ 盒的输入差分都非0。
第 4 轮轮函数的输出差分为 $D’ = l’ \oplus c’ = l’ \oplus a’ \oplus B’$ ,其中 $l’ = l \oplus l^$,已知。$a’ = 00000000$,$B’ = P(*0000000)$,其中 $$ 为未知的 4 比特向量,表示当第 2 轮轮函数中第一个 $S$ 盒 $S_1$ 的输入差分为 04(由于拓展变换)时可能的输出差分,未知。从而,第4轮轮函数中 8 个 $S$ 盒的输出差分为 $P^{-1}(D’)=P^{-1}(l’ \oplus P(0000000)) = P^{-1}(l’) \oplus (0000000)$,可求。故第四轮中$S_2,S _3,S _ 4, S _ 5, S _ 6, S _ 7, S _ 8$ 共 7 个$S$ 盒的输出差分均可求。
由上述两个步骤我们可以建立对7个$S$ 盒的差分分析模型,通过对$S$ 盒的差分分析,我们可以恢复 $7 × 6 = 42$ bit 的轮密钥,由密钥拓展算法,其他 $14$ bit 的密钥可通过穷尽搜索恢复。
上述攻击中我们未能恢复第 4 轮中进入第一个 $S$ 盒的密钥,是因为它的输出差分未知,因此我们可以选择另外的明文差分,让第二轮的输入差分经过拓展变换后导致第 1 个 $S$ 盒不活跃,即输入差分为0,这样我们就可求得第四轮中第 1 个 $S$ 盒得差分输出了。进而只用再穷尽搜索其他 $8$bit 密钥。
好的,上面大部分是《分组密码的攻击方法与实例分析》书中的原话。现在,我再用通俗易懂的话来翻译翻译。(也就是讲的再细一点啦)
笔者的“翻译”
我们看到,首先我们构造差分 $L’$为 20000000 ,$R’$ 为 00000000,这没什么问题,右下角的x脚标说明这是个十六进制表示,不过注意这里的$L’,R’$已经是$IP$ 置换过后的了,不是明文差分 $X’$ 的左右两部分哦,是$IP(X’)$的左右两部分。
然后我们这些个差分进入第一轮,右边的$a’=00000000$ 进到 $F$ 轮函数,由于是$00000000$,怎么线性非线性变换都没所谓,先$E$ 盒拓展,再轮密钥加,最后出了$S$ 盒也还是 $00000000$,再走一个$P$盒置换$P(00000000)$也还是 $00000000$。所以第一轮走完,左边差分等于 $A’ \oplus L’=00000000 \oplus 20000000=20000000$,右边还是原来的 $a’=00000000$
到了第二轮,这个轮函数的输入是 $b’ = A’ \oplus L’=20000000$,先先$E$ 盒拓展,变成40000000,然后分为八组进入$S$ 盒,显然后面 7 组都是0,不会激活 $S$ 盒,那出来还是0。(可能会突然疑惑,轮密钥加呢?看到最上面的差分经过 $F$ 函数各个组件的性质第一条,差分不受轮密钥加的影响,所以后面也都不管它了)但是第一组是以差分为 4 进入 $S$ 盒的,由于性质第三条,$S$ 盒的输出差分不确定,这与输出差分有关,也与具体的输出有关。所以,这一轮 $S$ 盒的输出差分为 *0000000,之后还得 $P$ 盒置换,所以$B’ = P(0000000)$。*那么第二轮走完*,左边等于$B’ \oplus R’ = P(0000000) \oplus 00000000=P(*0000000)$,右边等于$b’ = 20000000$
开始第三轮,这一轮开始就要乱起来了。首先这个轮函数的输入是 $c’ = B’ \oplus R’= P(*00000000)$,我们看一下具体的 $P$ 盒,
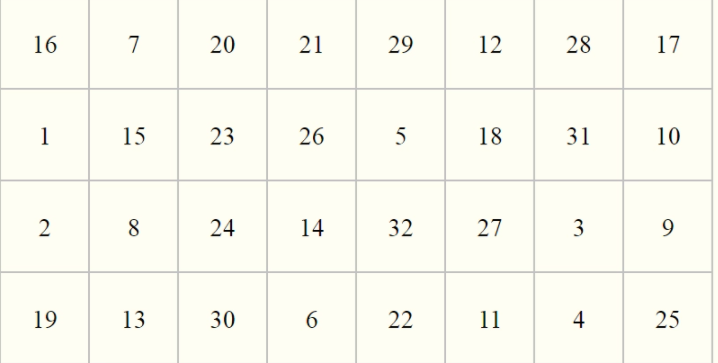
这里我们不确定的前四个bit被扩散到了第3,5,6,8组,也就是说现在我们的$c’ = 000**0$,然后这里还要先$E$ 盒拓展,看看 $E$ 盒
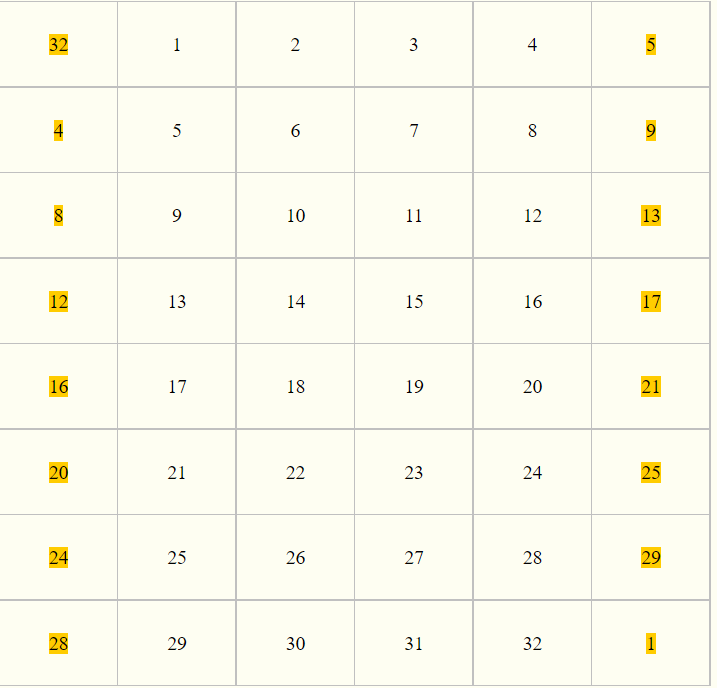
那么进入$S$ 盒前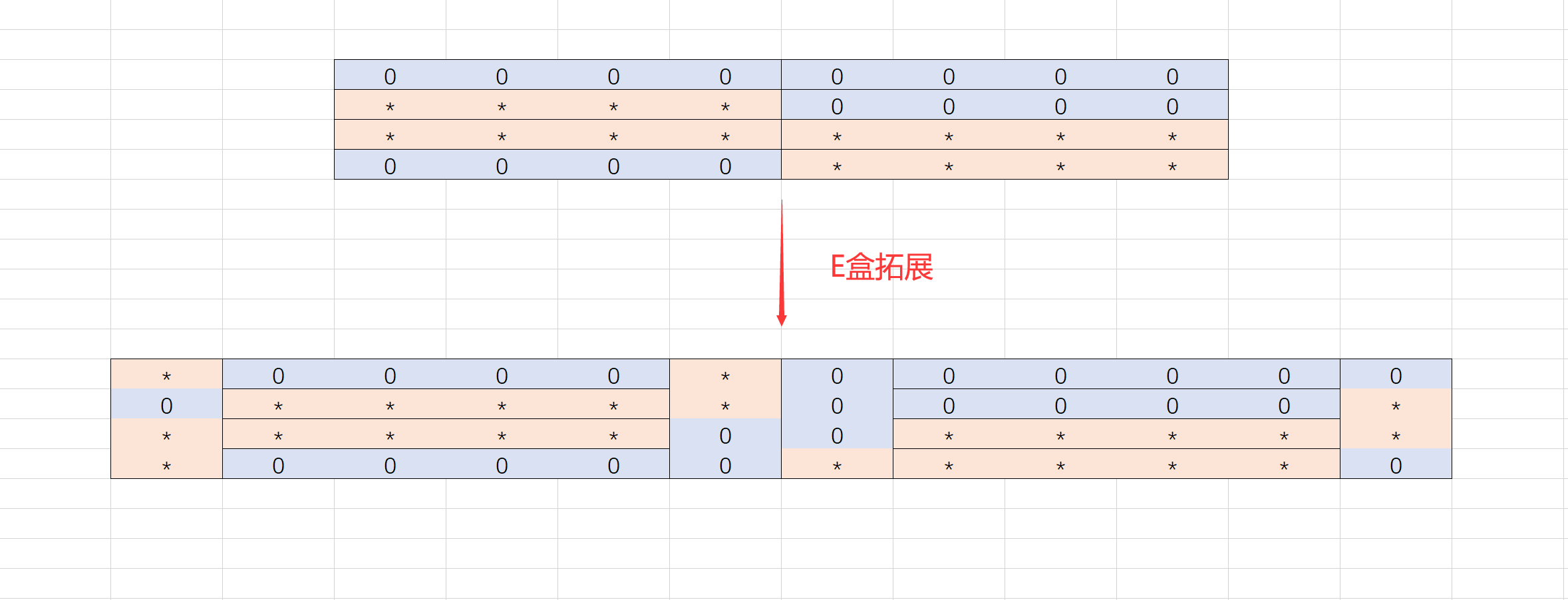
可以看到,几乎每一组都被”污染了“,只剩第5组还是 0 那么 $C’ = *0$,然后这里还有一个 $P$ 盒置换,那么第三轮走完,左边等于$C’ \oplus b’ = 20000000 \oplus P(*0)$,右边等于$c’ = *0$(注,这里 * 为不确定的意思,进入$S$ 盒前的 * 大概率不等于出 $S$ 盒后的 *)
到最后的第四轮了,此时进入 $S$ 盒的是$d’ = C’ \oplus b’$,万幸只有四轮,所以$d’ = r’$,由于$r’$ 是可由最后的输出密文右半部分求一个$IP$ 逆置换而来,因此,$d’$ 已知。
我们直接计算$d’$ 可以发现 $d’$几乎不会有 0 bit,也可以推一下,因为 $d’ = P(*0) \oplus 20000000$,而由于这个$P$ 盒置换,第5组最终也会被”污染“,那么可以预见,每一组进入 $S$ 盒的差分都被”污染“了,也就是说每一个 $S$ 盒都会被激活。这也就是书中所说的简单分析 $S$ 盒针对差分的扩散特性以及拓展变换 $E$ 的性质可知,第 4 轮轮函数的输入差分 $r’$ 也即 $d’$ 经过拓展变换 $E$ 后(成为 $S$ 盒的输入差分),$E(r’)$ 几乎会让 8 个 $S$ 盒 都活跃,即这个 8 个 $S$ 盒的输入差分都非0。
那么到此四轮DES分析完毕。其实也就说明了一个问题,进入第四轮的 $S$ 盒的输入会激活所有的 $S$ 盒,然后进入第四轮 $S$ 盒的输入差分已知,从第四轮后面7个 $S$ 盒出来的输出差分可求,由此我们可以建立对这7个$S$ 盒的差分分析模型以求出第四轮的轮密钥。
接下来简单讲讲具体怎么求。
首先拿到最后的输出明文差分 $Y’$,首先对右半边求 $IP$ 逆置换得到 $d’=r’$,然后对其用 $E$盒 做拓展置换。先打住,我们去求一下第四轮 $S$ 盒 的输出差分$P^{-1}(D’)$
我们拿到输出明文差分$Y’$,对做半边求 $IP$ 逆置换得到 $l’ = c’ \oplus D’$,这个$c’ = a’ \oplus B’ = 00000000 \oplus P(00000000) $,所以$P^{-1}(D’) = P^{-1}(c’ \oplus l’)=P^{-1}(a’ \oplus B’ \oplus l’) = P^{-1}(P(0000000) \oplus l’)$
好了,我们有了$S$盒输入差分$E(IP^{-1}(Y’_r))$,有了 $S$ 盒输出差分 $P^{-1}(P(*0000000) \oplus IP^{-1}(Y’_l)$,现在我们对每个 $S$ 盒开始爆破其相干的轮密钥分组了
第四轮的轮密钥会分为8组,分别和经过 $E$ 盒拓展置换的 8 组输入异或后最终进入 $S$ 盒。这8组输入差分在与轮密钥异或前后是不会变的,但是我们再次强调前面提到过的第三条性质:$S$ 盒:$S(x) \oplus S(x^) = y \oplus y^$,结果不确定,不仅与$x \oplus x^*$ 有关,还与 $x$ 有关。输入的差分没变,但是两次输入的具体值因为轮密钥的异或,会发生变化。因此改变这里的轮密钥,是会使得 $S$ 盒的输出差分受影响的。
但是呢,但是呢,我们不是已经知道输出差分了么?啊哈,那么很显然了,我们只要不断地尝试每个 $S$ 盒那一组的轮密钥——轮密钥加,再 $S$ 盒输出差分,然后对比我们已知的输出差分,如果匹配,则该轮密钥放入待选集合。由于每个 $S$ 盒只用到 6bit 轮密钥,因此穷举复杂度只有 $7× 2^6$,完全可以接受。然后会出现多解的情况。换一组具有相同差分(非必须,差分为40000000 00000000也可)的明文输入,得到一个新的解集,再取交集即可。根据实际情况,一般取四对差分明文就能有很大概率解出 42 bit的轮密钥。
然后现在有两个选择,一个是选择复杂度为 $2^{14}$ 穷举,另一个是换一下差分,不要激活到第一个 $S$ 盒就行。这样就能恢复全部的48 bit密钥,然后再进行复杂度为 $2^8$ 的穷举,两种复杂度倒也都是能接受的。
有了48bit的轮密钥后,我们知道密钥拓展用的压缩 $P$ 盒
- 所以我们先根据 $P$ 盒将 48 bit 的密钥位置先还原,
- 剩下的空位再直接穷举,最后得到56bit的轮密钥,
- 然后根据轮密钥生成的方式,将第四轮轮密钥还原成最初的密钥,
- 然后我们选取一对服务端生成的明文密文对,用我们的密钥对明文进行加密,
- 观察得到的密文是否与服务端生成的密文一致,若一致则得到正确密钥,否则回到第二步。
至此,4轮DES差分就到此结束了。可以看到,还没有用到概率论的知识,这是因为轮次比较少,前面我们分析的每一轮都是确定的,而等轮次增大到8轮以后就要开始引入统计分析与概率论了,取寻找概率较大的差分路径,这才是差分分析的完全体。
Remark:前面我们提到,DES差分分析的关键就在于其S盒差分分布的不均匀特性,何为不均匀特性,即相同的差分进入S盒,输出的差分是不均匀分布的。现在回头来看看这句话应该就能理解了,如果S盒差分分布均匀,相同地输入差分能够得到相同的输出差分,那么,我们就没办法去穷举验证我们的轮密钥了,因为我们没有了标准去区分密钥的正确与否。
结语
差分分析入门篇到此告一段落,希望接下来能有进阶篇叭,如果我学的会,能够理解的话哈哈哈哈哈哈哈哈哈哈哈哈哈。
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081,也可以邮件至 643713081@qq.com
文章标题:密码学学习笔记 之 差分分析入门篇——四轮DES
文章字数:3.7k
本文作者:Van1sh
发布时间:2021-07-16, 09:24:25
最后更新:2021-08-19, 21:12:42
原始链接:http://jayxv.github.io/2021/07/16/密码学学习笔记之差分分析入门篇——四轮DES/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

