密码学学习笔记 之 Coppersmith’s Method
首发于安全客
这一块咕咕咕了好久,暑假了,终于才有时间去细究coppersmith背后的原理。
前言
还记得自己刚入门CTF后打的第一个相对比较大的比赛就是2019届的强网杯,那个时候密码学就有一道copper study的题目。对于刚入门时来说,觉得那道题简直就是(无法形容)。后来才知道原来里面的每一关都可以在github上找到相应的脚本。但是当我想去找原理的时候,却发现,,,找不到。所以也才有了这篇文章。
Coppersmith’s Method
首先看看Coppersmith’s Method这玩意儿能干啥。简而言之,就是有一个函数,比如$F(x) = x^3+x+123$,然后有一个模数,比如 $M = 77$,然后假设存在一个$x_0$ 满足$F(x_0) \equiv 0 \pmod{M}$, 并且如果这个$x_0$小于某个特定的值,那么就可以用Coppersmith’s Method去找到这个$x_0$。【PS:想要实现这个手法还是需要掌握一点格基规约的相关知识的(至少知道格基规约是干啥的,结果输出的是啥)】
总的来说,如果能将M分解,那么找到这个$x_0$是容易的,用一个中国剩余定理即可;否则就是困难的。对应的,如果我们能够找到一个解满足$x^2 \equiv 1 \pmod{M}$ 并且这个x不等于$\pm 1 \pmod{M}$,那么我们用一个GCD就能将这个M给分解。具体可参考二十年以来对 RSA 密码系统攻击综述一文。因此,我们并不希冀于有一个有效的算法对于所有这样的同余式都能找到解,否则也就意味着大数分解问题破解了。
既然不能对所有的同余式都能找到解,那能找到解的条件是啥呢?对于度为$d$的多项式$F(x)$,如果$x_0$满足$F(x_0) \equiv 0 \pmod{M}$ 并且$|x_0|< M^{\frac{1}{d}-\epsilon}$,那么这个解$x_0$就能在多项式时间内被找到。
First Steps to Coppersmith’s Method
首先我们有在模M下的度为d的并且系数为整数的一个首一多项式:$F(x)=x^d+a_{d-1}x^{d-1}+\dots+a_1x+a_0$【如果多项式不是首一的,我们整体的系数乘上一个$a_d^{-1}$即可,如果$a_d$在模M没有逆元,那这条同余式可以拆成同余式组,但这并不是这篇文章讨论的重点】假设我们知道存在一个整数$x_0$满足$F(x_0) \equiv 0 \pmod{M}$ 并且 $|x_0|<M^{\frac{1}{d}}$,我们的任务就是找到这样的$x_0$。我们想,如果有这样一条多项式$G(x)$,他的解也是$x_0$。但是他的系数很小,导致$x_0$可以满足$G(x_0)= 0$【注意这里是等号,不是同于号】Coppersmith’s Method就是想办法去将这个$F(x)$变形为成为这样的$G(x)$。
example 1
假设$M=17 * 19=323$,$F(x)=x^2+33x+215$,我们想找到一个小根$x_0$满足$F(x_0)\equiv 0 \pmod{M}$【这里的$x_0=3$,但是在整数域下,$F(3)!=0$ 】
我们可以找到一个多项式$G(x) = 9\cdot F(x) -M\cdot(x+6)=9x^2-26x-3$ 满足$G(3)=0$,这个解可以直接用求根公式得到,如果次数比较大,也可以用牛顿迭代法。
好了,这就是一元Coppersmith’s Method核心思路了,其实一点也不难的吼。
接下来主要是对这个$x_0$的界的一些讨论以及如何尽量的提高这个界的一些手法。
我们定义$X$为这个$|x_0|$取值的上界,
然后我们将$F(x)$表示为一个行向量$b_F=(a_0,a_1X,a_2X^2,…,a_dX^d)$
Theorem 1(Howgrave-Graham)
首先我们有$F(x),X,M,b_F$这几个上面提到的值
也有$F(x_0)\equiv 0 \pmod{M}$
那么,当$||b_F||<\frac{M}{\sqrt{d+1}}$,则有$F(x_0) = 0$
proof
首先我们需要知道著名的柯西不等式 $(\sum_\limits{i=1}^{n}x_iy_i)^2≤(\sum_\limits{i=1}^{n}x_i^2)(\sum_\limits{i=1}^{n}y_i^2)$,
设$y_i=1,x_i≥0,1≤i≤n$,那么我们有$\sum_\limits{i=1}^{n}x_i≤\sqrt{n\sum_\limits{i=1}^{n}x_i^2}=\sqrt{n}||(x_1,…,x_i)||$
因而$|F(x_0)|=|\sum_\limits{i=1}^{d}a_ix_0^i|≤\sum_\limits{i=1}^{d}|a_i||x_0|^i≤\sum_\limits{i=1}^{d}|a_i|X^i≤\sqrt{d+1}||b_F||<\frac{\sqrt{d+1}M}{\sqrt{d+1}}=M$
所以$-M<F(x_0)<M$,又因为$F(x_0)\equiv 0 \pmod{M}$,所以$F(x_0)= 0 $
【这里不等式的第三个就用到了柯西不等式的性质】
这个定理对于确定$x_0$的边界值$X$很重要。
之前我们找到的G(x)我们直接给出的,现在开始说这个$G(x)$该怎么去找,首先我们考虑度为$d-1$的多项式$G_i(x) = Mx^i(0≤i<d) $,还有一个$F(x)$,显然,这里一共d+1条式子,他们的均有解$x = x_0 \pmod{M}$,我们将他们的系数向量组合成一个矩阵$B = \begin{bmatrix} M&0&\dots&0&0 \newline 0&MX&\dots&0&0 \newline \vdots&\vdots&\ddots&\vdots \newline 0&0&\dots&MX^{d-1}&0 \newline a_0 &a_1X&\dots &a_{d-1}X^{d-1}&X^d\end{bmatrix}$,$X$为$x_0$的取值上界
显然,这个矩阵的行列式为:$det(L)=M^dX^{d(d+1)/2}$
然后我们利用LLL算法做一个格基规约,然后设规约后的矩阵的第一行行向量为$b’$,这一点需要用到LLL的一个性质就是,
$||b’||≤2^{\frac{n-1}{4}}det(L)^{\frac{1}{n}}$,所以$||b’||≤ 2^{\frac{d}{4}}M^{\frac{d}{d+1}}X^{\frac{d}{2}}$
为了满足Theorem 1,故要求$2^{\frac{d}{4}}M^{\frac{d}{d+1}}X^{\frac{d}{2}}<\frac{M}{\sqrt{d+1}}$,移项一下可得$2^{\frac{d}{4}}\sqrt{d+1}X^{\frac{d}{2}}<M^{\frac{1}{d+1}}$
如果d=2,那么$X≈M^{\frac{1}{3}}$,如果d=3,那么$X≈M^{\frac{1}{6}}$。
至此,我们初步的有了一个$X$的取值范围,但这还并未达到$M^{\frac{1}{d}-\epsilon}$的程度。。。
example 2
设M=10001,多项式$F(x)=x^3+10x^2+5000x-222$,【这里其实我们已经提前知道$x_0 = 4$,所以满足$x_0 < M^{\frac{1}{6}}$】
这里我们设$x_0$的上界$X=10$,所以我们构造格$B = \begin{bmatrix} M&0&0&0 \newline 0&MX&0&0 \newline 0&0&MX^{2}&0 \newline -222 &5000X&10X^2&X^3\end{bmatrix}$,利用LLL规约后我们可以得到第一行(the first row)为$(444,10,-2000,-2000)$,所以我们找到多项式$G(x)=444+x-20x^2-2x^3$,来个牛顿迭代法求根可得$x_0=4$
The Full Coppersmith Method
这里回顾一下example 2,即使以$M^{\frac{1}{6}}$来计算边界也应该是4.3左右,那为什么我们设X=10最终也可以得到正确的结果呢?其实审视一下整个过程,我们最终的目的只是为了获得一组系数,最后规约出来的行向量也都做了相应的”去除X“处理,所以这里对X的取值其实并不用特别严格。
其次,如果不取这个约来的边界$M^{\frac{1}{6}}$,而是直接将d=3带入$2^{\frac{d}{4}}\sqrt{d+1}X^{\frac{d}{2}}<M^{\frac{1}{d+1}}$来计算这个x的边界,其实边界值应该是2.07左右。嗯?还是那个问题,那为啥我们可以得到正确结果呢?因为其实这个边界值也并不是很严格,在推导得出这个值的时候本身就用了很多次不等式,再者,我们利用的LLL中的那个性质,$||b’||≤2^{\frac{n-1}{4}}det(L)^{\frac{1}{n}}$,我们取的是LLL算法规约出来的最坏的情况,而大多数情况得到的结果要比这值小许多。
回到这一章的主题,在上一章中我们对X的取值有不等式:$2^{\frac{d}{4}}M^{\frac{d}{d+1}}X^{\frac{d}{2}}<\frac{M}{\sqrt{d+1}}$,稍微还原一下是$2^{\frac{n-1}{4}}M^{\frac{d}{n}}X^{\frac{d(d+1)}{2n}}<\frac{M}{\sqrt{n}}$,所以想要增加X就有两个思路,一个是往矩阵里多加几行向量来增加格的维度$n$,第二个就是增大$M$了。【这两个方法在公式层面看起来可能不那么直观,公式还需要再变形一下,并且应该也会有一个最优解】
针对第一种方案,我们称这种往格里插入的,增加了格的维度而不增加M的多项式为:“x-shift” polynomial,它们是$xF(x),x^2F(x),…,x^kF(x)$,显然这些多项式在M下的解也为$x_0$。
针对第二种方案,我们可以利用$F(x)$的幂来增加M,因为$F(x_0) \equiv 0 \pmod{M}$,则有$F(x_0)^k \equiv 0 \pmod{M^k}$
我们继续拿上文中的example 2来举例,之前我们用到的格的维度n=4,所以d=3,带入那条不等式我们可以得到$2^{\frac{3}{4}}(M^3X^6)^{\frac{1}{4}}<\frac{M}{\sqrt{4}}$,带入$M、X$可得$X≈2.07$,现在我们往格中添加两个多项式$xF(x),x^2F(x)$,得到
$B = \begin{bmatrix} M&0&0&0&0&0 \newline 0&MX&0&0&0&0 \newline 0&0&MX^{2}&0&0&0 \newline -222 &5000X&10X^2&X^3&0&0 \newline 0&-222X&5000X^2&10X^3&X^4&0 \newline 0&0&-222X^{2}&5000X^3&10X^4&X^5 \end{bmatrix}$
现在我们格的维度为6,并且行列式为$M^3X^{15}$,带入那条不等式可得$2^{\frac{5}{4}}(M^3X^{15})^{\frac{1}{6}}<\frac{M}{\sqrt{6}}$,现在算出来$X≈3.11$,可以看到通过添加“x-shift” polynomial,我们确实增大了X。
这里有一个现成的结论就是通过添加“x-shift” polynomial:$ xF(x),x^2F(x),…,x^{d-1}F(x)$,我们可以使得$X≈M^{\frac{1}{2d-1}}$,所以当d=3,通过“x-shift” polynomial,我们将$X≈M^{\frac{1}{6}}$ 提升为$X≈M^{\frac{1}{5}}$。那么如果在此基础上再增加了M呢?
Theorem 2 (Coppersmith)
设$0<\epsilon <min{0.18,\frac{1}{d}} $,$F(x)$为度为d的首一多项式,如果其在域$M$下有一个或多个根$x_0$满足$|x_0|<M^{\frac{1}{d}-\epsilon}$,那么我们就可以在与$d,\frac{1}{\epsilon},log(M)$相关的多项式时间内找到它,
proof
设$h>1$,构造一个格$L$,用过多项式:$G _ {i,j}(x)=M^{h-1-j}F(x)^jx^i,(0≤i<d,0≤j<h)$,注意到$G _ {i,j}(x_0)\equiv 0 \pmod{M^{h-1}}$,那么格L的维度就是$dh$,其行列式$det(L)=M^{\frac{(h-1)hd}{2}}X^{\frac{(dh-1)dh}{2}}$
【这里可能看着比较抽象,没事,待会下面会有个例子】
此时我们运用LLL算法进行规约,我们得到第一行的行向量$b’$,其满足$||b’||<2^{\frac{dh-1}{4}}det(L)^{\frac{1}{dh}}=2^{\frac{dh-1}{4}}M^{\frac{h-1}{2}}X^{\frac{dh-1}{2}}$
由于这里的域M已经提升为$M^{h-1}$,这里我们再用上Theorem 1,从而有$\sqrt{dh}2^{\frac{dh-1}{4}}M^{\frac{h-1}{2}}X^{\frac{dh-1}{2}}<M^{h-1}$,
变形一下为:$\sqrt{dh}2^{\frac{dh-1}{4}}X^{\frac{dh-1}{2}}<M^{\frac{h-1}{2}}$
这里我们换元一下,设$c(d,h)=(\sqrt{dh}2^{\frac{dh-1}{4}})^{\frac{2}{h-1}}=\sqrt2(dh)^{\frac{1}{dh-1}}$,那么我们有$c(d,h)X<M^{\frac{h-1}{dh-1}}$
注意到${\frac{h-1}{dh-1}}=\frac{1}{d}-\frac{d-1}{d(dh-1)}$,我们设$\epsilon = \frac{d-1}{d(dh-1)}$,那么有$h=\frac{\frac{d-1}{d \epsilon}+1}{d}≈\frac{1}{d\epsilon}$,并且$dh=\frac{d-1}{d \epsilon}+1$,所以$c(d,h)=\sqrt2(\frac{d-1}{d \epsilon}+1)^{\frac{d\epsilon}{d-1}}$,当$\epsilon $趋向于0时,$c(d,h)$趋向于$\sqrt2$,
因为之前我们有$c(d,h)X<M^{\frac{h-1}{dh-1}}$,用上$\epsilon$就是$c(d,h)X<M^{\frac{1}{d}-\epsilon}$,所以这里咱如果想要达到Coppersmith定理的那个效果,那么我们需要$c(d,h)≤2$,这里我们再次换元,设$\alpha=\frac{d\epsilon}{d-1}$,那么$c(d,h)=\sqrt2(\frac{1}{\alpha}+1)^\alpha$,所以我们要求$(\frac{1}{\alpha}+1)^\alpha≤\sqrt2$,因为$\epsilon = \frac{d-1}{d(dh-1)}≤ \frac{d-1}{d}$,所以$\alpha≤1$,所以解得$0≤\alpha≤0.18$,
结合上面提到的:$0<\epsilon <min{0.18,\frac{1}{d}} $,由于$0≤\alpha=\frac{d\epsilon}{d-1}≤0.18$,并且$\frac{1}{d}-\epsilon >0$,所以当$d>5$时,$\epsilon < \frac{1}{d}$,当$0<d≤5,\epsilon<0.18$,
运行LLL算法用时肯定是跟格的维度,格里面数值大小有关的,又由$h=\frac{\frac{d-1}{d \epsilon}+1}{d}≈\frac{1}{d\epsilon}$,所以格L的维度$dh≈\frac{1}{\epsilon}$,所以时间复杂度与$d,\frac{1}{\epsilon},log(M)$有关。这里也有一个结论就是,Coppersmith‘s Method的一个大致的时间复杂读为$O((\frac{1}{\epsilon})^9log(M)^3)$,
example 3
设$p=2^{30}+3,q=2^{32}+15,M=pq$
$F(x)=a_0+a_1x+a_2x^2+a_3x^3=1942528644709637042 + 1234567890123456789x + 987654321987654321x^2 + x^3$
并且我们事先知道根:$|x_0|≤2^{14}$,所以我们设$X=2^{14}$,注意到$X≈M^{\frac{1}{4.4}}$。这里我们构造格$L = \begin{bmatrix} M^2&0&0&0&0&0&0 \newline 0&M^2X&0&0&0&0&0 \newline 0&0&M^2X^{2}&0&0&0&0 \newline Ma_0 &Ma_1X&Ma_2X^2&MX^3&0&0&0 \newline 0&Ma_0X&Ma_1X^2&Ma_2X^3&MX^4&0&0 \newline 0&0&Ma_0X^{2}&Ma_1X^3&Ma_2X^4&MX^5 &0\newline a_0^2&2_0a_1X&(a_1^2+2a_0a_2)X^2&(2a_0+2a_1a_2)X^3&(a_2^2+2a_1)X^4&2a_2X^5&X^6\end{bmatrix}$
注意到,我们这里并没有像proof中的那样,加上所有的$G _ {i,j}(x)$,这里我们只添加量两条“x-shift” polynomial,额外添加了一条$F(X)^2$,第四行为$MF(X)$。理论上我们还可以针对$F(X)^2$再添加两条“x-shift” polynomial,但这里并没有这么做,是综合考虑了到$x_0$的上界X,和LLL算法运行的时间复杂度。所以这里格的维度是7,行列式$det(L)=M^9X^{21}$。
这里运行LLL算法,并将第一行的行向量的相应X值去除得到系数向量,可得$G(x)=-369928294330603367352173305173409792 + 88565517701781911148679362207202x
-3439987357258441728608570659x^2 + 446358057645551896819258x^3
+4564259979987386926x^4 - 1728007960413053x^5 - 21177681998x^6$
运算求根算法可得$x_0=16384$
到这里,我们对于单元Coppersmith’s Method的原理学习就告一段落了。至于最初说的$x_0$的取值上界可以达到$M^{\frac{1}{d}-\epsilon}$,而为啥最后我们证明出来的是却是$\frac{1}{2}M^{\frac{1}{d}-\epsilon}$。从Coppersmith 定理的证明过程来看,应该是与$\alpha$的取值范围有关。
实例-第三届强网杯之copper study
第一关:Stereotyped messages
已知n,e=3,c,m共512bit但是低72bit未知,原理可参考Mathematics of Public Key Cryptography ch19。也即前文所述。
1 | [+]Generating challenge 1 |
这道题我们完全可以将题面转化为在求方程$f(x) = (m+x)^3$ 在模N下的解
所以可以直接套我们前面所描述的方法
exp:
1 | # 展示格的样式 |
构造的格的样式

与example3 是类似的
但其实sage已经集成了coppersmith的求根方法,因此简单调用一下函数就可以解决这个问题。这里之所以这样做其实是想映照前文,展示一下利用coppersmith来解决此类问题的整个过程。
利用现成方法版exp
1 | N = |
BTW,这里泄露的是明文的高位,其实还有泄露低位、泄露高低位的情况。但换汤不换药,无非是由$m+x$变成了$ m_h +x * 2^k + m_l$。
第二关:Factoring with high bits known
已知n,e,c,n=pq且已知p的高位
1 | [+]Generating challenge 2 |
这一关我们需要引入一个新的定理
Theorem 3
设$N=p * q $并且有$p<q<2p$,设$0<\epsilon<\frac{1}{4}$,如果满足关系:$|p-p’|≤\frac{1}{2\sqrt2}N^{\frac{1}{4}-\epsilon}$,那么给定N和p’,我们就可以在与$log(N)$和$\frac{1}{\epsilon}$相关的时间复杂度内分解N。
这里我就不再给出令人头大的证明了。直接给出一个例子,但是显然,由于条件的改变,这个格子的构造也会与之前的格子不同。
example 4
设$N=16803551,p’=2830 , X=10.$
我们设$F(x)=(x+p’)$,并且考虑多项式:$N, F(x),xF(x)=(x^2+p’x),x^2F(x)$。然后构造格
$B = \begin{bmatrix} N&0&0&0 \newline p’&X&0&0 \newline 0&p’X&X^{2}&0 \newline 0 &0&pX^2&X^3\end{bmatrix}$
LLL规约后得到第一行的SVP为(105,-1200,800,1000),去除X可以得到
$G(x)=x^3+8x^2-120x+105$;解方程可以得到$x=7$,检查一下确实 $2387|N$
【这里的$N$也许显得突兀,把它看作是$k * p$也许会好理解些:所选取的多项式带入正解$x$时均在模$p$下与0同余。】
除了这样构造格子,通过查阅网上关于这道题的题解可以发现另一种格子的构造。我们这里是“x-shift”了三次,另外那种是先提升次数,然后再“x-shift”,具体用了这八个多项式:$N^4, N^3F(x), N^2F(x)^2,NF(x)^3,F(x)^4,xF(x)^4,x^2F(x)^4,x^3F(x)^4$
格子的样式:
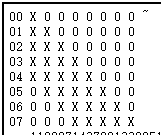
之所以这么选也是这里新引入了两个参数,一个是beta,一个是t,beta是未知p与已知N指数关系,这里就是0.4,因为$p≈N^{0.4}$,【其实可以是0.5,但我们并不确定$p,q$的大小关系,保险起见用0.4】t的具体取值与beta相关,另外这里的h的取值也与beta有关,X的取值也与上面的定理所述不同。
exp
1 | # 展示格的样式 |
这个脚本其实也可以用在第一关,只要将beta改成1,再带入相应的多项式和数据就可以了。
相关的paper和原脚本在github,有兴趣的师傅可以研究研究。
同样,利用现成函数版exp
1 | N = |
BTW,同第一关一样,这里的p泄露了高位,但与p泄露了低位的情况,无差。
第三关:Partial Key Exposure Attack
已知n,e=3,c,d的低512bit已知 【n的长度为1023】
1 | [+]Generating challenge 3 |
根据RSA相关参数我们可以知道的是$e * d = k\phi(n)+1$,
我们设 $s = p + q$,
则有$e *d = k(n-s+1)+1$。
再设$d$的低位为$d_0$ ,与$n^{\frac{1}{2}}$约为一个bit长度级别,
设n的bit长度为$L$,由$e *d = k(n-s+1)+1$我们很容易能得到
$e * d_0 \equiv k(n-s+1)+1 \pmod{2^{\frac{L}{2}}}$ ①,
接下来的操作可能有点跳跃:这里我们想消元,把上式的s给消去,又因为我们有
$p^2-sp+n = p^2-p^2-pq+n=0$ ②
$p * ①-k * ②=ed_0p\equiv kpn-kps+kp+p-kp^2+kps-kn\equiv kpn + kp+p-kp^2-kn \pmod{2^{\frac{L}{2}}}$
这样式子就只有一个未知数$p$了,即解同余式方程:
$ed_0x\equiv knx + kx+x-kx^2-kn \pmod{2^{\frac{L}{2}}}$
我们就可以得到$p$的低位$p_0$了。
不对,我们似乎漏了$k$的值,但是由最初的$e*d = k\phi(n)+1$我们可以知道,$d<\phi(n)$,那肯定有$k<e$,而这里$e=3$,所以爆这个$k$就完事。
然后我们再用第二关的脚本,梭他就完事。
exp源自
1 | def recover_p(p0, n): |
第四关:Hastad’s Broadcast Attack
已知n1,c1,n2,c2,n3,c3,e=3
1 | [+]Generating challenge 4 |
对于这一关,由于我们知道$m$是512bit的,而用于加密的$e$等于3,因此三个$c$即为$m^3$ 在不同模下的剩余。由于$m^3为512 * 3=1536bit$,而可以知道的是三个模n的bit长度分别为1021,1023,1024。所以利用中国剩余定理【具体原理可以看俺这一篇文章】我们是可以还原长度为$1536bit$的$m^3$的,最后我们再开个三次根就好得到$m$了。
exp
1 | from gmpy2 import * |
但既然这里讲的是coppersmith‘s method,那么我们再来看看如何用coppersmith‘s method来解决这道低指数广播攻击的问题。
我们再看到这个问题,我们有三条式子,分别是
$m^3\equiv c_1 \pmod{n_1}$
$m^3\equiv c_2 \pmod{n_2}$
$m^3\equiv c_3 \pmod{n_3}$
然后前面的方法是我们用了一个CRT,求得到了一个C 满足$m^3 \equiv C \pmod{N}$,其中$N=\prod_{i=0}^{3}n_i $,而由于N过大,导致这个同余式等同于等式,因此我们才可以直接对C开三次根,求得m。
而用coppersmith‘s method来解决这道问题,我们可以将问题推广到更一般的情况,就是加密的不再是相同的m,而是具有线性关系的$m_i$,比如:$e = 3,m_i = m,m+1,2m+2 $我们就有三条式子
$m^3\equiv c_1 \pmod{n_1} => f(m)=m^3-c_1\equiv 0 \pmod{n_1}$
$(m+1)^3\equiv c_2 \pmod{n_2} => f(m)=(m+1)^3-c_2\equiv 0 \pmod{n_2}$
$(2m+2)^3\equiv c_3 \pmod{n_3} => f(m)=(2m+2)^3-c_3\equiv 0 \pmod{n_3}$
同样,由于这里的$n_i$彼此互素,因此利用CRT我们最终也能得到一个式子$f(x) \equiv 0 \pmod{N}$
m显然会是这个式子的解,而又由于$m<N^{\frac{1}{3}}$,因此利用coppersmith‘s method我们可以求解得m。
exp来自食兔人的博客——CTF中的RSA基本套路
1 | Cs = [] |
第五关:Related Message Attack
已知n,e=3,m对应的密文c1,(m+1)对应的密文c2
1 | [+]Generating challenge 5 |
同第四关一样,这一题也有多解,一种是像一叶飘零师傅这篇文章所述,直接硬化公式
exp
1 | import gmpy |
另一种是求多项式下的GCD,
首先这一题我们可以将已知的信息转换一下,我们设$M_1 = m$,$M_2 = m+1$;再变换一下,设$M_1=x$,那么$M_2 = ax+b $ 【$a=b=1$】
如果我们有映射关系$f(x)=ax+b$,那么就有$M_2 = f(M_1)$,因此题面
$m^3-c_1 \equiv 0 \pmod n$
$(m+1)^3-c_2 \equiv 0 \pmod n$
可以变成求解一个方程组
$X^3-c_1 \equiv 0 \pmod n$ ①
$f(X)^3-c_2 \equiv 0 \pmod n$ ②
显然对于这两个多项式有一个公共解:$M_1$,因此两条式子都可以化成
$(X - M_1) * K_1 \equiv 0 \pmod n$
$(X-M_1) * K_2 \equiv 0 \pmod n$ 【$K_i$代表未知的多项式】
再由①、②式的单调性可知,①、②式在实数域下仅由唯一解,因此$K_1、K_2$式均不可再因式分解,因此其彼此互素
从而我们对这两个多项式求一个GCD就可以得到$(X-M_1)$,但由于在模$n$下,得到的将是$X+M’$的形式 【$M’ \equiv -M_1 \pmod n$】,所以最终$M = -M’ \pmod n$
exp
1 | def franklinReiter(n,e,b,c1,c2): |
第六关:Boneh Durfee Attack
已知n,e,c,d只有1024 * 0.27bit
1 | [+]Generating challenge 6 |
继续来推式子:
$∵ed=k\phi(n)+1$
$∴k\phi(n)+1\equiv 0 \pmod{e}$
$∴k(N+1-p-q)+1\equiv 0 \pmod{e}$
$∴2k(\frac{N+1}{2}+\frac{-p-q}{2})+1\equiv 0 \pmod{e}$
设$A=\frac{N+1}{2},y=\frac{-p-q}{2}),x=2k$,可得式子:$f(k,y)=1+x * (A+y)$
如果我们能在模$e$下解得该方程的根$x,y$,由$ed=1+x * (A+y)$就可以得到$d$了。
但具体怎么去求解这个方程呢?这就涉及多元coppersmith’s method了,超纲了吖,所以这里先用了github上的一个脚本boneh_durfee.sage。这里的适用条件是$d<N^{0.292}$
思考&总结
在coppersmith’s method的边界计算中,由于推理中存在的不等式,格基规约算法在不同情况有不同的表现等问题,导致coppersmith’s method的边界其实比较模糊,而构造不同的格也会计算出不同的边界值,有不同的效果。所以,在考虑时间和空间复杂度的情况下,是否会存在某种最优的构造方法呢?
好了,这里大概是大部分的对单元coppersmith’s method的应用实例了。最后一手Boneh Durfee Attack利用了多元coppersmith‘s method,这算是埋了一手伏笔么?
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081,也可以邮件至 643713081@qq.com
文章标题:密码学学习笔记 之 Coppersmith’s Method
文章字数:7.6k
本文作者:Van1sh
发布时间:2020-08-13, 10:00:00
最后更新:2021-06-02, 16:41:04
原始链接:http://jayxv.github.io/2020/08/13/密码学学习笔记之coppersmith/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

