关于微信公众号

浅尝Lattice 之 HNP

首发于安全客

前言

  格密码是一类备受关注的抗量子计算攻击的公钥密码体制。而格理论也使许多现代公钥密码RSA、DSA等体系受到影响。这篇文章主要从两道CTF题目来学习格密码中的HNP(Hidden number problem）。

Lattice

  首先谈谈个人对Lattice的理解叭。个人觉得，Latiice就是由若干线性无关的向量组成的一个向量空间，在这个空间中，向量彼此之间可以进行相应的加、减运算。向量也可以乘以某个系数，但这个系数仅限于整数，因而形成了布满整个空间的格点。在格中的计算问题主要包括两种，即SVP(the Shortest Vector Problem of lattice)和CVP(the Closest Vector Problem)，然后个人认为，CVP可以给Latiice加上一个维度后变成SVP，继而可以用LLL算法来进行规约从而找到最短向量。

XCTF2020-高校战役-NHP

题目附件

题目信息

题目用的是DSA公钥密码签名系统。

题目提供签名函数：用户以用户名注册，服务端返回签名，并提供所用临时密钥的bit长度

我们需要以admin的身份登陆来获取flag，但是服务端不会给admin签名

解题流程

根据题目流程，显然，我们要利用临时密钥的bit长度来获取私钥，从而获得admin的签名

其中，我们知道的信息全局公钥p, q, g，服务端公钥y , 每轮签名使用的r, s, 以及我们可控的H(x)，x即为用户名，Hash函数这里用的是sha256

step1-公式转化

由DSA签名中各参数的关系

$r \equiv g^k \pmod{q}$
$s \equiv k^{-1}(H(m) + xr) \pmod{q}$

可得每轮临时密钥与签名、明文的关系

$k_i \equiv s_i^{-1}r_i \cdot x + s_i^{-1}H(m) \pmod{q} $
$k_i \equiv A_i x + B_i \pmod{q} $
$k_i = A_i x + B_i + l_i q$

其中$k_i$就是每次使用的临时密钥

化简后的式子中的$A_i,B_i$均可由已知信息计算

step2-构造Lattice

对于上式中的$k_i$，我们仅仅知道它的bit_ength，bit_ength泄露了什么信息呢？

当我们知道一个数的bit_ength时，我们能确定这个数的大小范围，

比如一个数的bit_ength是500时，我们能确定这个数大小落在$(2^{499}-1,2^{500}-1]$

所以我们知道这个数的MSB位为2^499

这等价于，我们知道了临时密钥的一个大概的值，我们设其为$K$

然后我们构造Lattice

$M =
\begin{bmatrix}
q & & & & & & \newline
& q & & & & & \newline
& &\ddots& & & & \newline
& & & q & & & \newline
A_1&A_2&\dots & A_t&K/q& & \newline
B_1&B_2&\dots & B_t& & K & \newline
\end{bmatrix}$

然后这里就会存在一个向量 $v =
\begin{bmatrix}
l_1 & l_2 & \cdots & l_t & x & 1
\end{bmatrix}$

使得

$vM =
\begin{bmatrix}
l_1 & l_2 & \cdots & l_t & x & 1
\end{bmatrix}
\begin{bmatrix}
q & & & & & & \newline
& q & & & & & \newline
& &\ddots& & & & \newline
& & & q & & & \newline
A_1&A_2&\dots & A_t&K/q& & \newline
B_1&B_2&\dots & B_t& & K & \newline
\end{bmatrix} = \begin{bmatrix}
k_1 &
k_2 &
\cdots &
k_t &
Kx/q &
K
\end{bmatrix}
= v_k$

其中向量$v$中的x即为我们的私钥，

step3-LLL

解决格密码的问题LLL算法的运用总是必不可少的，可是这里我们该如何利用LLL算法去找到向量$v_k$呢？

如果我们的$v_k$的长度在格中很小，我们利用LLL就很可能将其找出。所以，我们需要与服务端交互，然后收集当$k_i$的bit_length比较小的情况时的相关数据。比如：我们知道q的bit_length为128，那我们可以找bit_legnth为122的$k_i$，然后我们还需要一定的数据量，这样能提高利用LLL算法找到这个短向量的概率，并且，上述格中$K/q, K$的构造也是为了让$v_k$中的每一项的长度都差不多，这样也有利于找到$v_k$，参考这一篇文章中的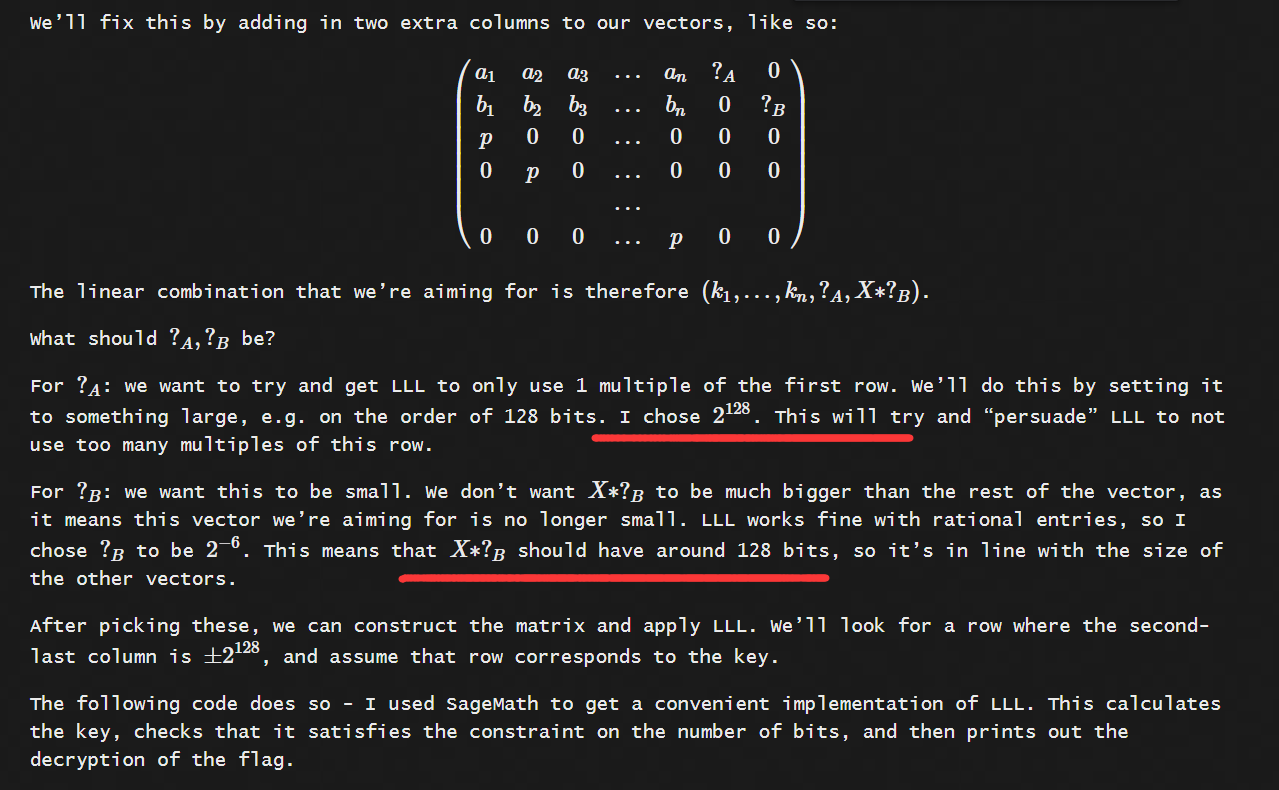

参考祥哥博客的这篇出题文章，另外感谢祥哥的解惑。

NPUCTF2020-babyLCG

题目附件可以在BUUOJ下载

题目流程

1. 初始化一个LCG加密类，用到随机参数a, b, m, seed，其中a, b, m，均在附件给出
2. 生成20个128位的随机数，但是只给出每个数的高64位
3. 再生成三个随机数，用AES加密加密flag，key由前两个随机数组成，分别取第一个随机数和第二个随机数的高64位拼起来，iv由第三个随机数组成

解题思路

从题目流程来看，我们目的只有一个，恢复seed。

step1-公式转化

LCG生成随机数的公式为：$s_{i+1} = a*s_i+b\pmod{m}$

但是这一题，我们只知道$s_1$ 到$s_{20}$的高64位，所以我们将$s_i$分为h、l高低位两部分，其中$h_i$已知。所以有

$(h_{2}+l_{2}) \equiv a*(h_1 + l_1 )+b\pmod{m}$

$l_{2} \equiv a * l _ 1+a * h _ 1+b-h _ {2}\pmod{m}$

$l_{2} \equiv A _ 1 * l _ 1+B _ 1\pmod{m}$ 【$设A _1 = a; B _ 1 = a * h _ 1+b-h _ {2}$】

$l _ {3} \equiv a * l _ {2}+a * h _ {2}+b-h _ {3}\pmod{m}$

$l _ {3} \equiv a * A_1 * l _ {1}+a * B_1+a * h_{2}+b-h _ {3}\pmod{m}$

$l _ {3} \equiv A _ {2} * l _ {1}+B _ {2}\pmod{m}$【$设A _ {2} = a * A _ 1; B _ {2} = a * B _ 1+a * h _ {2}+b-h _ {3}$】

…

这里，我们通过公式的变形，可以将原来式子$s _ {i+1} = a*s _ i + b \pmod{m}$

中$s_{i+1}和s_{i}$的关系转变为$l_{i+1}和l_{i}$的关系。当然，原系数a、b的意义也发生了对应转变。

这里给出生成新A 和B 的脚本

b=153582801876235638173762045261195852087
a=107763262682494809191803026213015101802
m=226649634126248141841388712969771891297

h = [0,7800489346663478448,11267068470666042741,5820429484185778982,6151953690371151688,548598048162918265,1586400863715808041,7464677042285115264,4702115170280353188,5123967912274624410,8517471683845309964,2106353633794059980,11042210261466318284,4280340333946566776,6859855443227901284,3149000387344084971,7055653494757088867,5378774397517873605,8265548624197463024,2898083382910841577,4927088585601943730]
for i in range(len(h)):
	h[i] <<= 64
A = [1]
B = [0]
for i in range(1, len(h)-1):
	A.append(a*A[i-1] % m)
	B.append((a*B[i-1]+a*h[i]+b-h[i+1]) % m)
print(A[1:])
print(B[1:])

step2-构造Lattice

现在我们二十条与 $l_1$ 相关的方程组了。即

$l_{i+1} \equiv A_i*l_1+B_i\pmod{m}$

$l_{i+1} = A_i*l_1+B_i+k_im$

且对于 $l_i$ 我们真的一无所知么？我们其实知道 $l_i$ 是小于2^64的，即 $l$ 最大为64bit。这样与前面一道题就很类似了。

于是我们构造Lattice

$M =
\begin{bmatrix}
m & & & & & \newline
& m & & & & \newline
& &\ddots& & & \newline
& & & m & & \newline
A_1&A_2&\dots & A_{19}&1& \newline
B_1&B_2&\dots & B_{19}&0& 2^{64}\newline
\end{bmatrix}$

然后这里就会存在一个向量 $v =
\begin{bmatrix}
k_1 & k_2 & \cdots & k_{19} & l_1 & 1
\end{bmatrix}$ 使得

$vM =
\begin{bmatrix}
k_1 & k_2 & \cdots & k_{19} & l_1 & 1
\end{bmatrix}
\begin{bmatrix}
m & & & & & \newline
& m & & & & \newline
& &\ddots& & & \newline
& & & m & & \newline
A_1&A_2&\dots & A_{19}&1& \newline
B_1&B_2&\dots & B_{19}&0& 2^{64} \newline
\end{bmatrix} = \begin{bmatrix}
l_2 &
l_3 &
\cdots &
l_{20} &
l_1 &
2^{64}
\end{bmatrix}
= v_l$

其中$l_1$即为$s_1$的低位，拼上其高位，在利用a, b, m就能恢复seed了

step3-LLL

  这里我们的$v_l$向量每一位都只有约64bit，显然，它是整个格中比较短的向量了，且我们一共有19组数据，那么直接对这个Lattice M运用LLL算法就可以找到$v_l$了。（格中参数$2^{64}$的选取道理与上面一致）

完整exp：

'''
#sage
b=153582801876235638173762045261195852087
a=107763262682494809191803026213015101802
m=226649634126248141841388712969771891297

h = [0,7800489346663478448,11267068470666042741,5820429484185778982,6151953690371151688,548598048162918265,1586400863715808041,7464677042285115264,4702115170280353188,5123967912274624410,8517471683845309964,2106353633794059980,11042210261466318284,4280340333946566776,6859855443227901284,3149000387344084971,7055653494757088867,5378774397517873605,8265548624197463024,2898083382910841577,4927088585601943730]
for i in range(len(h)):
	h[i] <<= 64
A = [1]
B = [0]
for i in range(1, len(h)-1):
	A.append(a*A[i-1] % m)
	B.append((a*B[i-1]+a*h[i]+b-h[i+1]) % m)
A = A[1:]
B = B[1:]


M = matrix(ZZ, 21, 21)

for i in range(19):
    M[i, i] = m
    M[19, i] = A[i]
    M[20, i] = B[i]
    M[i, 19] = M[i, 20] = 0
M[19, 19] =  1
M[20, 20] = 2^64
M[19, 20]= 0


#print(B)
vl = M.LLL()[0]
l1 = vl[-2]
h1 = h[1]
s1 = l1+h1
#s1 = a*seed+b %m
seed = ((s1 - b)*inverse_mod(a,m))%m
print(seed)

'''
#python
from Crypto.Util.number import *
from Crypto.Cipher import AES

class LCG:
	def __init__(self, bit_length):
		b = 153582801876235638173762045261195852087
		a = 107763262682494809191803026213015101802
		m = 226649634126248141841388712969771891297
		seed = 73991202721494681711496408225724067994
		self._key = {'a':a, 'b':b, 'm':m}
		self._state = seed
        
	def next(self):
		self._state = (self._key['a'] * self._state + self._key['b']) % self._key['m']
		return self._state
    
	def export_key(self):
		return self._key


def gen_lcg():
    rand_iter = LCG(128)
    key = rand_iter.export_key()
    f = open("key", "w")
    f.write(str(key))
    return rand_iter


def leak_data(rand_iter):
    f = open("old", "w")
    for i in range(20):
        f.write(str(rand_iter.next() >> 64) + "\n")
    return rand_iter


def encrypt(rand_iter):
    f = open("ct", "wb")
    key = rand_iter.next() >> 64
    key = (key << 64) + (rand_iter.next() >> 64)
    key = long_to_bytes(key).ljust(16, b'\x00')
    iv = long_to_bytes(rand_iter.next()).ljust(16, b'\x00')
    cipher = AES.new(key, AES.MODE_CBC, iv)
    pt = flag + (16 - len(flag) % 16) * chr(16 - len(flag) % 16)
    ct = cipher.encrypt(pt.encode())
    f.write(ct)

def decrypt(rand_iter):
    with open("ct", "rb") as f:
    	flag = f.read()

    key = rand_iter.next() >> 64
    key = (key << 64) + (rand_iter.next() >> 64)
    key = long_to_bytes(key).ljust(16, b'\x00')
    iv = long_to_bytes(rand_iter.next()).ljust(16, b'\x00')
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ct = cipher.decrypt(flag)
    print(ct)


def main():
    rand_iter = gen_lcg()
    rand_iter = leak_data(rand_iter)
    decrypt(rand_iter)


if __name__ == "__main__":
    main()

总结

  从这两题我们可以发现，解决HNP问题，一般我们需要多组数据，然后每一组就像方程组中的每一条方程，我们根据这些方程组构造一个Lattice，也可以认为是一个矩阵，就好像在用矩阵解决线代中的 XA=B 的问题，这个B中的每一项是我们获得的MSB这样子的比较模糊的信息（上面两题我们拿到的都是未知量的bit_length，也相当于MSB）。然后这个B向量的长度（范式）需要相对与格中其他向量要短，然后我们就可以利用LLL算法找到这个B，进而根据我们的构造，确定X向量中我们需要的一个特定的值。也就是方程组的解。

  需要再次说明的是，这个矩阵所代表的方程组并非像真正的线代中的XA=B问题中的方程组——是多元的。我们这里的方程组是一元的。如果正常解方程的话，之所以这么多条方程都算不出解，就是因为我们得到信息是模糊的，并非是准确的。故我们需要用到格理论，和一个超好用的LLL算法。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com