密码学学习笔记 之 分组密码操作模式

Van1sh 密码小屋/ Block 操作模式
创建时间:
字数:5.6k 阅读:
  1. 前言
    1. 操作模式
      1. 电子密码本模式（EBC）
        1. 缺陷
        2. 代换攻击
        3. 防御
        4. CTF中EBC相关的题目-2019OGeek-Babycry
      2. 密码分组链接模式(CBC)
        1. 缺陷
        2. CBC反转字节攻击（Modification attack on CBC）
        3. CTF中CBC反转字节攻击 应用场景
        4. Padding Oracle Attack
      3. 密码反馈模式(CFB)
        1. 缺陷
        2. 重放攻击
        3. CTF中的CFB模式相关的题目-hgame2020-week3-Feedback
      4. 输出反馈模式(OFB)
        1. 缺陷
      5. 计数器模式(CTR)
        1. 缺陷
  2. 总结
  3. 参考

首发于合天智汇

前言

  最近在分组密码学习的过程中，了解了AES分组密码以及分组密码的五种操作模式。目前已知的对AES的分析攻击都比蛮力攻击的复杂度要高。所以这里我们跳过AES加密本身，看看这五种操作模式的原理以及是否会因为一些操作不当而产生弱点。

操作模式

  分组密码不仅仅是一个加密算法，也是用于实现多种不同密码学编码机制的万能元件。例如，人们可以使用分组密码构建各种不同种类的基于分组的加密方案，甚至还可以用它来实现序列密码。其中，不同的加密方式就称为操作模式。目前包括五种主流的操作模式：

电子密码本模式(electronic code book mode, ECB)
密码分组链接模式(cipher block chaining mode, CBC)
密码反馈模式(cipher feedback mode, CFB)
输出反馈模式(output feedback mode, OFB)
计数器模式(Counter mode, CTR)

电子密码本模式（EBC）

  电子密码本模式是一种最直接的消息加密方式，

假设$e_k()$表示用密钥k进行的分组加密；$e_k^{-1}()$对应解密。

$x_i$，$y_i$表示长度为b的位字符串，（长度不够的字符串会按照指定的填充规则进行填充）

加密：$y_i=e_k(x_i) ,i≥1 $ $(e_k()$表示用密钥k进行的分组加密)

解密：$x_i=e_k^{-1}(y_i) ,i≥1 (e_k^{-1}()$表示用密钥k进行的分组加密的解密)

  电子密码本模式就是最简单的一一映射加密，这意味着每一组的加密都是独立的，所以EBC模式加密可以实现并行化，这种方式在高速实现中具有很强的优势。并且，如果由于传输问题导致消息中间有一段数据受影响，也不会影响到后面的消息，这与后面要提到的CBC,CFB等模式是不同的。

缺陷

  正因为EBC模式的一一映射加密，每一组加密相互独立，所以同样的明文用同样的密钥就会加密得到同样的密文。下面介绍EBC模式下的一种简单攻击方式：

代换攻击

假设某个协议支持银行间的电汇，电汇包含五个字段，分别有五个分组

代换攻击

首先一个前提是我们能监听，拦截并更改这个电汇的密文，

然后我们可以先开个账户，进行若干次试验，每一次变更一个参数，比如发送账号，转账金额，一组密码的位数等，以此来确定每一个分组的意义。

等我们大概知道五个分组的意义后，我们就能进行替换攻击。比如银行A的某个账户向银行B的某个账户转账，我我们将其拦截，把接受账号密文代换成事先存好的我们账号的密文，则银行用key解密后，就会把钱都转到我们的账户下。值得一提的是，整个过程我们并没有攻击分组密码本身，所以尽管加密方案本身再安全也抵御不了这种攻击；我们甚至也不知道真正明文的内容，所以实现代换攻击是破坏了消息的完整性。

例子很特殊，比如五个参数刚好在五个分组等，只是为了方便理解_

防御

现实中抵御代换攻击常用消息验证码(Message Authentication Code, MAC)，和数字签名，主要就是为了确保消息的完整性。

CTF中EBC相关的题目-2019OGeek-Babycry

前面提到，分组加密中长度不够的字符串会按照指定的填充规则进行填充，再加上ECB这样一一映射的明文-密文对关系，就会产生利用pad来逐位爆破明文的攻击。

nc 过去得到加密规则

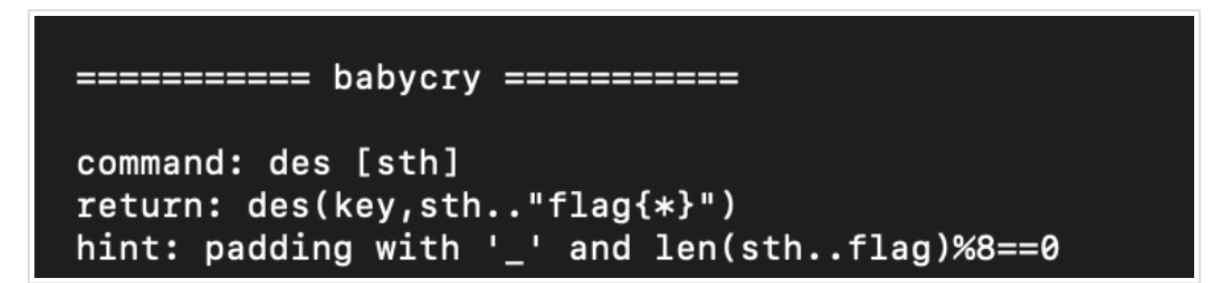
Babycry

加密规则是des（key,sth..flag{*}padding）   （模式可以类比为ECB的一一映射）

加上hint

所以我们控制输入，可以使得被加密的字符末尾为

1
}_______（7个_）

比如key加上flag是50位，并且flag以‘}’ 结尾。他是8位一组，那么我们就填上7个a，这样key+sth+flag就有57位，八位一组，前面56位字符分8组，于是最后一组加上填充就是}_______（7个'_'）

然后服务器会返回给我们密文，于是密文的最后一组就代表着}_______（7个'_'）的密文，

如果我们再多填一个a，那么返回密文中最后一组就是?}______（6个'_'）的密文①（’?’代表flag的最后到数第二位字符，未知，需要爆破）

于是我们就开始爆破，我们先测出key的长度先，（看填几个a会密文会多出一组来就能知道）

然后填a，让 len(key)+len(a)%8 == 0，接着，我们就发送aaa*}______（6个'_'）,（a的个数由key的长度决定，*代表任意字符，我们直接遍历可见字符表）让服务返回加密结果，我们找到明文对应的那一组密文，和之前返回的密文①做比较，结果一样，说明那位字符正确，开始爆破下一位字符。

以此类推可以逐位爆破出所有位字符。（只是爆破超过八位后，用来作为判断依据的密文①就不能再从密文最后一组找了，得从到数第二组，第三组….找_）

密码分组链接模式(CBC)

在CBC模式中，后一组的密文都受前一组密文影响，第一组密文受初始向量IV影响，从而明文的重复排列不会反应在密文中。

假设$e_k()$表示用密钥k进行的分组加密；$e_k^{-1}()$对应解密。

$x_i，y_i$表示长度为b的位字符串，IV表示长度为b的初始向量，（长度不够的字符串会按照指定的填充规则进行填充）

*加密：$y_1=e_k(x_1 ⊕ IV)$ **

   $y_i=e_k(x_i⊕ y_{i-1}) ,i≥2 $

*解密：$x_1=e_k^{-1}(y_1)⊕ IV$ **

   $x_i=e_k^{-1}(y_i) ⊕ y_{i-1} ,i≥2$

  如果每次加密是都选择一个新的IV，则CBC模式就变成了一个概率加密方案，即相同的明文加密会生成不同的密文。

  需要说明的是，如果每次选择IV的数值得当，则代换攻击会彻底失效，因为监听者无法识别加密的模式。但是如果若干次加密使用相同的IV，则监听者还是可以识别加密模式。

  虽然（承接ECB的例子）这一次直接将我们的账户的密文替换上去已经不能实现向我们账户转账的效果，因为我们代换，会导致第四、五组消息都被破坏，但是有可能解密后，账户和金额仍然具有意义呢？（虽然可能性似乎很低）只是是随机的，不再可控了而已。但这仍然是银行所不可接受的。所以消息验证码和数字签名的作用显得尤为重要。

缺陷

因为某些原因，使得某一组密文中出现了错误的bit，将影响这一组(整组)及其之后一组(相应位)分组的解密。由此产生了CBC反转字节攻击。另外与下面所讲的CFB模式一样，CBC模式也不能抵御重放攻击。

CBC反转字节攻击（Modification attack on CBC）

Modification attack on CBC

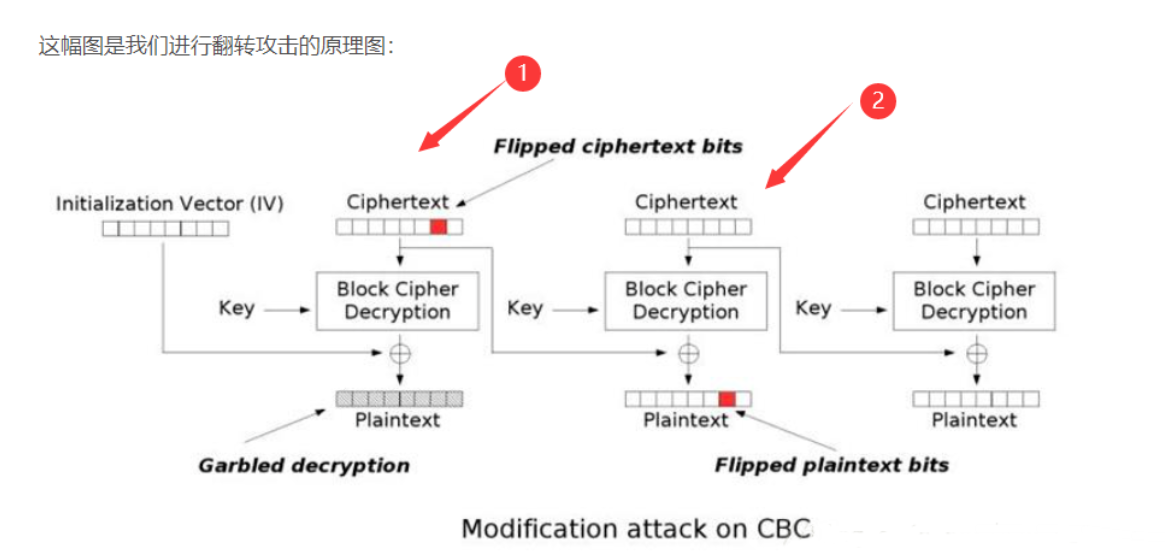
在加密时，前一组明文会影响后面所有分组的密文。

但是在解密时，由公式及原理图可知，一组密文只会影响这一组的解密结果和下一组的解密结果。

我们看到箭头2，这一组Ciphertext（密文2）在Decryption（解密）之后会生成Ciphertext_1（我yy的），然后这个Ciphertext_1与箭头1所指的Ciphertext（密文1）按位异或后最终生成Plaintext（明文2）

所以我们可以修改Ciphertext1，来达到控制Plaintext2的效果，当然如果想要精确控制，则需要知道Plaintext2的具体内容。（在某些特定条件下，Plaintext2的内容可以利用Padding Oracle Attack 来获取，下文会简略介绍这种攻击方式）

并且由于Ciphertext1的修改，导致自己这一组的解密会受影响，所以还需要修改图中的IV来给Ciphertext1“擦个屁股”。（如果前面不是IV呢？那只能一路改下去，直到IV为止了。。。）

CTF中CBC反转字节攻击 应用场景

​ CBC反转字节攻击可能会用于Web题中的绕过。比如一个登陆，然后在传输过程中是将你提交的信息用分组密码加密，模式是CBC，然后到服务端后再解密。

  提交的时候他不让你填写admin，但是题目又需要你有admin的身份。这个时候就可以考虑用CBC反转字节攻击绕过过滤。

  比如：先用bdmin的身份登陆，然后拦截、更改身份对应密文组的前一组的对应位，让服务器将身份解密成明文后为admin，但是身份前一组的明文应该是毁掉了，那就再改前一组的密文来进行补救，直到改到初始向量IV为止。

Padding Oracle Attack

这里粗略介绍一下CBC模式下的Padding Oracle Attack

  在AES加密的CBC模式中，若加密数据的长度模除分块长度而有余，则会在末尾填充一组数据。

即(pad_length-len(data)%pad_length)*hex(pad_length-len(data)%pad_length)

举个栗子（8字节一组）

1
2
3
4
5
6
7
8
9
10
11
12
数据：
aaaaa
填充后的数据：
aaaaa\x3\x3\x3
数据：
aaaaaaaaaa
填充后的数据：
aaaaaaaaaa\x06\x06\x06\x06\x06\x06
数据：
aaaaaaaa
填充后的数据：
aaaaaaaa\x08\x08\x08\x08\x08\x08\x08\x08

​ Padding Oracle Attack 需要两个前提就是：

1.可以控制密文 或者 IV

2.如果解密后不满足 padding 服务端会报错. （只有最后一个块长度不足时会有填充）

再次举栗子：

  此处选择了AES-128作为例子，明文长度为17位，故补齐至32位后分2组进行加密。

  然后我们伪造一组IV来和第一组密文一起发回服务器，让其进行判定。

1
2
3
明文：southseastisacat!
IV：\x31\x32\x33\x34\x35\x36\x37\x38\x38\x37\x36\x35\x34\x33\x32\x31
密文：\xbf\x61\xb3\x1b\xd3\x6a\x47\x11\xb9\xcc\xd7\x11\x7b\x8a\x42\xd9\x3a\x1e\x37\xe9\xd2\xde\xfa\xca\xa2\x50\xfd\xc0\x6e\xf2\x11\xc1

  对IV的最后一位字符进行爆破，构造0x00到0xff，使得第一组密文的最后一个字节解密的结果同IV异或结果为0x01，导致Padding通过，当IV最后一位字符是0x44时，服务器返回正确结果。

  这时IV的最后一个字节和原IV的最后一个字节还有0x01异或，即0x44^0x31^0x01，得到结果为t，是第一组明文的最后一个字符。

  然后可以固定IV的最后一个值使得第一组密文的最后一个字节解密的结果同IV异或结果为0x02，此时爆破IV到数第二个字节，当第一组密文的到数第二个字节解密的结果同IV异或结果为0x02时，服务器返回正确结果，此时又能确定第一组明文的倒数第二个字符，以此类推_

密码反馈模式(CFB)

与CBC类似，CFB模式每一组的密文也会影响后续所有组的密文，直接看加解密规则吧

假设$e_k()$表示用密钥k进行的分组加密；

$x_i，y_i$表示长度为b的位字符串，IV表示长度为b的初始向量（不需要填充）

加密：$y_1=e_k(IV)⊕x_1$

   $y_i=e_k(y_{i-1})⊕x_i ,i≥2$

解密：$x_1=e_k(IV)⊕y_1$

   $x_i=e_k(y_{i-1})⊕y_i ,i≥2$

  加密上面确实感觉挺像，只是$x_i$和⊕在括号里还是在括号外的区别。但正因为这点小小的区别，导致解密上CFB模式仍然用的是分组加密的加密函数。

  类似“CBC翻转字节攻击”，在CFB上也可进行类似的控制，只不过这次“擦屁股的人”是这一组密文后面的所有密文组了。

缺陷

与CBC类似，因为某些原因，使得某一组密文中出现了错误的bit，将影响这一组(相应位)及其之后一组(整组)分组的解密。CFB模式也不可抵御重放攻击。

重放攻击

举个栗子：

​ Alice向Bob发送一条消息，这条消息由4个密文分组组成。主动攻击者Mallory将该消息中的后3个密文分组保存了下来。第二天，Alice又向Bob发送了内容不同的4个密文分组（假设Alice使用了相同的密钥）。攻击者用昨天保存下来的3个密文分别将今天发送的后3个密文分组进行了替换。

  于是，Bob解密时，4个分组中只有第1个可以解密成正确的明文分组，第2个会出错，而第3个和第4个则变成了被攻击者替换的内容（也就是昨天发送的明文内容）。攻击者没有破解密码，就成功地用以前的电文混入了新电文中。而第2个分组出错到底是通信错误呢，还是被人攻击所造成的呢？Bob是无法做出判断的。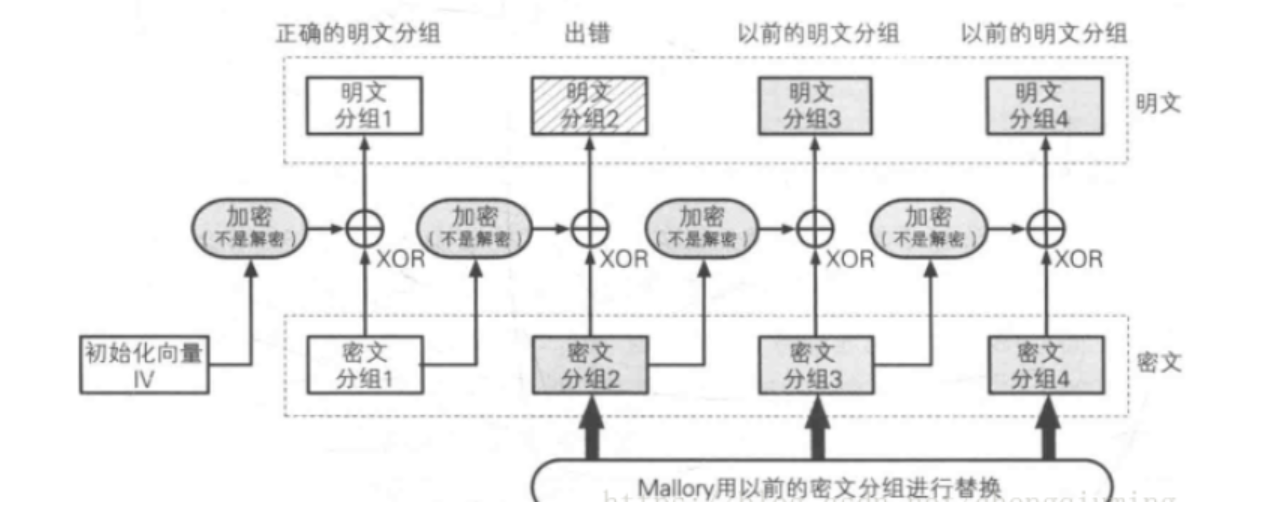
重放攻击

CTF中的CFB模式相关的题目-hgame2020-week3-Feedback
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import os, random
import string, binascii
import signal
import socketserver
from hashlib import sha256
from Crypto.Cipher import AES

from secret import MESSAGE
assert len(MESSAGE) == 48


class Task(socketserver.BaseRequestHandler):
    def __init__(self, *args, **kargs):
        self.KEY = b""
        self.IV = b""
        super().__init__(*args, **kargs)

    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline: msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'> '):
        self.send(prompt, newline=False)
        return self._recvall()

    def encrypt(self, data):
        assert len(data) % 16 == 0
        aes = AES.new(self.KEY, AES.MODE_CFB, self.IV, segment_size=128)
        return aes.encrypt(data)

    def decrypt(self, data):
        assert len(data) % 16 == 0
        aes = AES.new(self.KEY, AES.MODE_CFB, self.IV, segment_size=128)
        return aes.decrypt(data)

    def handle(self):
        signal.alarm(60)
        self.KEY = os.urandom(32)
        self.IV = os.urandom(16)

        self.send(b"You have only 3 times to decrypt sth, then I'll give u the FLAG.")
        try:
            for _ in range(3):
                self.send(b"Give me sth(hex) to decrypt")
                hex_input = self.recv()
                if not hex_input:
                    break
                ciphertext = binascii.unhexlify(hex_input)
                plaintext = self.decrypt(ciphertext)
                self.send( binascii.hexlify(plaintext) )
        except:
            self.send(b"Rua!!!")
            self.request.close()

        enc_msg = self.encrypt(MESSAGE)
        self.send(b"Here is your encrypted FLAG(hex): ", newline=False)
        self.send( binascii.hexlify(enc_msg) )
        self.request.close()


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass

if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 1234
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

可搜集到的信息：

MESSAGE (flag) 的长度为48位，三组，每组16位。

程序的功能：AES加密，CFB模式。每次连接会随机生成一个IV和key，然后最多可以对我的输入进行三次解密，最后会把flag用同样的IV和key加密，然后发送给我们。

解题思路：

首先列出加密解密的流程，由于只有三组，都写出来会比较好看些。

Feedback

需要搞清楚的是，在三次解密阶段，我们的输入是图中左侧的y1,y2,y3；在flag加密阶段，flag是图中右侧的f1,f2,f3

步骤1：拿第一段flag(称为flag1)：

既然程序会对我们的输入进行解密，我们发送一串与flag密文等长的密文过去，程序解密后返回一段明文。

看到解密第一条，我们只需要将明文和密文的前16字节逐位异或就能得到$e_k(IV)$的值。

而三次解密之后程序返回的flag的密文的第一组就是flag1与$e_k(IV)$异或的结果。所以我们拿着$e_k(IV)$同flag的密文的第一组异或就能得到flag1。

步骤2：拿第二段flag(称为flag2)：

看到加密那一侧，flag2是flag的明文同$e_k(y_1)$异或的结果，那么我们的目的就是拿到$e_k(y_1)$

我们现在是手持flag1的人，我们现把将要发送的48字节划分为三段，flag1：pad1：pad2

在经过第一次解密后，我们的得到的结果的组成是：

flag1与$e_k(IV)$异或的结果f1

pad1与$e_k(flag1)$异或的结果f2

pad2与$e_k(pad1)$异或的结果f3

这里我们需要转变思想的是，在加密阶段，flag1与$e_k(IV)$异或的结果就是y1，所以我们现在已经拿到y1了

然后我们只需要将我们要发送的48字节划分为三段：y1：pad1：pad2

我们得到的结果的组成就是：

y1与$e_k(IV)$异或的结果f1

pad1与$e_k(y1)$异或的结果f2

pad2与$e_k(pad1)$异或的结果f3

现在，我们只需要将f2和pad1异或就能提取出$e_k(y1)$了。然后就可以拿去解密flag2了。

步骤3：拿第三段flag(称为flag3)

现在我们是手持flag1和flag2的人了。为了拿到flag3，我们需要拿到上图右侧的$e_k(y2)$

而上图右侧y2是flag2和$e_k(y1)$异或的结果，flag2我们有了，$e_k(y1)$我们也能拿到，那就没啥困难了。

首先重复第二步骤的操作拿到$e_k(y1)$，然后我们将$e_k(y1)$和flag2异或得到y2

然后我们发送的48字节的组成为：pad1：y2：pad2

这样我们得到的结果的组成就是：

pad1与$e_k(IV)$异或的结果f1

y2与$e_k(pad1)$异或的结果f2

pad2与$e_k(y2)$异或的结果f3

现在我们只需要将f3和pad2异或就能提取出$e_k(y2)$了。然后就可以拿去解密flag3了。

输出反馈模式(OFB)

​ OFB模式形成了一个同步序列密码,因为此密钥序列既不依赖明文，也不依赖密文。同CFB模式相同是，接收者不需要使用分组密码的解密函数来解密密文。

加解密规则

假设$e_k()$表示用密钥k进行的分组加密；

$x_i，y_i，s_i$表示长度为b的位字符串，IV表示长度为b的初始向量（不需要填充）

加密：$s_1=e_k(IV) 且y_1=s_1⊕x_1$

   $s_i=e_k(s_{i-1}) 且y_i=s_i⊕x_i ,i≥2$

解密：$s_1=e_k(IV) 且x_1=s_1⊕y_1$

   $s_i=e_k(s_{i-1}) 且x_i=s_i⊕y_i ,i≥2$

OFB模式并不是通过密码算法对明文间接进行加密的，而是通过将“明文分组”和“密码算法的输出”进行XOR来产生“密文分组”的，在这一点上OFB模式和CFB模式十分类似。

而且OFB 可事前进行加密、解密的预备。与ECB不同的是，虽然每一组加密也相互独立，但明文的重复排列不会反应在密文中。因为一般情况下每次加密都会使用新的IV，所以使得OFB能够抵御重放攻击

缺陷

由于每一组的加解密独立，这降低了反转字节这样的主动攻击的成本。（不需要找”擦屁股的人“了）

计数器模式(CTR)

感觉上是OFB模式的升级版

加解密规则：

假设$e_k()$表示用密钥k进行的分组加密；

$x_i，y_i$表示长度为b的位字符串，初始值IV和计数器$CTR_i$的连接表示位表示为(IV || $CTR_i$也是一个长度为b位的位字符串（不需要填充）

加密： $y_1=e_k(IV || CTR_i) ⊕x_1 ，i≥1$

解密： $x_1=e_k(IV || CTR_i) ⊕y_1 ，i≥1$

解释一下这个密钥序列是如何生成：

  比如128位的AES。首先选择一个IV,长度小于分组长度(比如96位)。而剩下的32位则由计数器使用，并且该计数器的CTR值初始化为0。在会话期间加密的每个分组，计数器都会递增而IV则保持不变。在本例中，在不更换IV的情况下可加密的最大分组个数为$2^{32}$。由于每个分组长度都是8个字节，所以在生成一个新的IV前，可以加密的最大数据大小为$8*2^{32}=2^{35}$字节，大概为32G字节。

  与OFB模式和CFB模式一样，CTR模式的密钥序列也是分组计算，但最吸引人的一个特点就是可以并行化，因为计数器模式不需要任何反馈，这与OFB或CFB模式完全不同。所以，我们可以让两个分组密码引擎同时并行工作，即让两个引擎同时使用第一个分组密码加密计数器值CTR和CTR2。 等这两个分组密码引擎完成后，第一个引擎将继续加密值CTR3,而另一个引擎则继续加密CTR,如此循环。

  这种方案的加密速率是单个实现方式的两倍。当然，也可以同时运行多个分组密码引擎，这也会使加密速率按比例增加。对吞吐率要求严格的应用而言，比如在要求几Gb/s数据率的网络中，并行化的加密模式非常合适。

缺陷

与OFB模式相同，降低了反转字节这样的主动攻击的成本。

总结

  总的来说，感觉现在用的比较多的还是CBC加密模式，CTF中OFB加密模式和CTR加密模式的赛题也不常见。

  但对分组加密的五种主流加密模式及其一些攻击手法的学习，可以让我们了解这五种模式的各自的优缺点，这样，就算在以后的CTF的赛题中遇到，我们也好有的放矢。

参考

《深入浅出密码学——常用加密技术原理与应用》（清华大学出版社）

https://blog.csdn.net/csu_vc/article/details/79619309

https://blog.csdn.net/chengqiuming/article/details/82355772

https://www.dazhuanlan.com/2019/09/02/5d6c9d6f823a7/

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com

赏

文章标题:密码学学习笔记 之 分组密码操作模式

文章字数:5.6k

本文作者:Van1sh

发布时间:2020-03-03, 15:15:00

最后更新:2020-05-29, 12:41:10

原始链接:http://jayxv.github.io/2020/03/03/密码学学习笔记之分组密码操作模式/

版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

©2020 Van1sh

Built with Hexo and 3-hexo theme

目录
×

喜欢就点赞,疼爱就打赏