密码学学习笔记 之 数论四大定理及应用
首发于安全客
前言
可以发现RSA中的很多攻击方法都是从数论四大定理推导出的,所以找时间好好学习了一下数论四大定理的证明及其应用场景——Rabin算法。
欧拉定理
若$n,a$为正整数,且$n,a$互素,即$gcd(a,n) = 1$,则
$a^{φ(n)}\equiv1\pmod{n}$
证明
首先,我们需要知道欧拉定理是什么:
数论上的欧拉定理,指的是
$a^{φ(n)}\equiv1\pmod{n}$
这个式子实在$a$和$n$互质的前提下成立的。
证明
首先,我们知道在1到$n$的数中,与n互质的一共有$φ(n$)个,所以我们把这$φ(n)$个数拿出来,放到设出的集合X中,即为$x_1,x_2……x_{φ(n)}$
那么接下来,我们可以再设出一个集合为M,设M中的数为:
$m_1=a∗x_1,m_2=a∗x_2……m_φ(n)=a∗x_{φ(n)}$
下面我们证明两个推理:
一、M中任意两个数都不模n同余。
反证法。
证明:假设M中存在两个数设为$m_a,m_b$模$n$同余。
即$m_a\equiv m_b$
移项得到:$m_a−m_b=n∗k$
再将m用x来表示得到:$a∗x_a−a∗x_b=n∗k$
提取公因式得到:$a∗(x_a−x_b)=n∗k$
我们现在已知$a$与$n$互质,那么式子就可以转化为:
$x_a−x_b\equiv 0 \pmod{n}$
因为$a$中没有与$n$的公因子(1除外)所以$a !\equiv 0 \pmod{n}$ 所有只能是$ x_a−x_b\equiv 0\pmod{n}$。
又因为$x_a,x_b$都是小于$n$的并且不会相同,那么上述的式子自然全都不成立。
假设不成立。
证得:$M$中任意两个数都不模$4$同余。
二、M中的数除以n的余数全部与n互质。
证明:我们已知$m_i=a∗x_i$
又因为$a$与$n$互质,$x_i$与$n$互质,所以可得$m_i$与$n$互质。
带入到欧几里得算法中推一步就好了。
即:
$gcd(a∗xi,n)=gcd(mi,n)=gcd(n,mi mod n)=1$
证毕。
三、根据我们证得的两个性质,就可以开始推式子了。
首先,根据前两个推论可以知道,$M$中的数分别对应$X$中的每个数模$n$同余。
(即是双射关系:首先M中的数在模n下不同余,即不相同,然后有$φ(n)$个$m$;其次有$φ(n)$个不相同的$x$与$n$互质,所以$m$与$x$是双射关系)
所以可以得到:
$m_1∗m_2∗……∗m_{φ(n)}\equiv x_1∗x_2∗……∗x_{φ(n)}\pmod{n}$
现在我们把替换成x的形式,就可以得到:
$a∗x_1∗a∗x_2∗……∗a∗x_{φ(n)}\equiv x_1∗x_2∗……∗x_{φ(n)}\pmod{n}$
$a^{φ(n)}∗(x_1∗x_2……∗x_{φ(n)})\equiv x_1∗x_2……∗x_{φ(n)}\pmod{n}$
$(a^φ(n)−1)∗(x_1∗x_2……∗x_{φ(n)})\equiv 0\pmod{n}$
然后,由于$(x_1∗x_2……∗x_{φ(n)}) !\equiv 0\pmod{n}$
所以 $(a^{φ(n)}−1)\equiv 0\pmod{n}$
所以 $a^{φ(n)}\equiv 1\pmod{n}$
应用:RSA的解密
欧拉定理在RSA中可用于证明 $M\equiv C^d \pmod{N}$ :

费马小定理(欧拉定理特殊型情况)
对于质数p,任意整数a,均满足:$a^{p-1}\equiv 1 \pmod{p}$
那么,$a^{p-2}$就是a在模p下的逆元了
孙子定理(中国剩余定理 CRT)
设正整数$m_1,m_2…m_k$两两互素,则同余方程组
$x \equiv a_1 \pmod{m_1}$
$x \equiv a_2 \pmod{m_2}$
$x \equiv a_3 \pmod{m_3}$
…
$x \equiv a_k \pmod{m_k}$
有整数解。并且在模$M = m_1 \cdot m_2 \cdot … \cdot m_k$下的解是唯一的,解为
$x \equiv (a_1M_1M_1^{-1} + a_2M_2M_2^{-1} + … + a_kM_kM_k^{-1}) \mod M$
其中$M_i = M / m_i$,而$M_i^{-1}$为$M_i$模$m_i$的逆元。
证明
具体证明如下:
例:找出所有整数x,使其被3,5和7除时,余数分别为2,3和2
$x\equiv 2 \pmod{3}$
$x\equiv 3 \pmod{5}$
$x\equiv 2 \pmod{7}$
=> $x = △ + 357*t$ (△为期中的一个解,t为整数)
在同余中最重要的观念就是求出第一个解,那么$x = △ + 357*t$就是通解。那怎么求一个解呢?
利用同余的加性:
把$x$拆成$a+b+c$,即$x = a + b + c $
令
$a\equiv 2 \pmod{3}$
$a\equiv 0 \pmod{5}$
$a\equiv 0 \pmod{7}$
=> $a=35p$ ( 可以看到p取1的时候满足$a\equiv 2\pmod{3}$,即$a=35 $)
为何这样取?从接下来的取法可知:b 和 c 都会取 3 的倍数,这样子就能保证,x mod 3 = 2,我们标记这样的取法为FLAG
接下来要求b:
$b\equiv 0\pmod{3}$
$b\equiv 3\pmod{5}$
$b\equiv 0\pmod{7}$
=>$b=21q$ (可以看到q取3的时候满足$b\equiv 3\pmod{5}$,即$b=63$)
求c
$c\equiv 0\pmod{3}$
$c\equiv 0\pmod{5}$
$c\equiv 2\pmod{7}$
$=>$$c=15m$(可以看到m取2的时候满足$c\equiv 2\pmod{7}$,即$c=30$)
得
$x\equiv 2\pmod{3} \equiv a + b + c$
$x\equiv 3\pmod{5} \equiv a + b + c$
$x\equiv 2\pmod{7} \equiv a + b + c$
a b c 都求出来之后,可以利用同余的加性
$x = a + b + c = 128$是一个解, $x = 128 + 105t $在适当调整$t$之后就可以求出$x$在任何范围内的解,比如说求最小正整数解,这时候$t$取$-1$,得$x=23$
利用同余的乘性:
之前令$x = a + b + c$,用同余的乘性之后$x = 2a’ + 3b’ + 2c’$ (此时令$a’=b’=c’=1$,就相当于同余的加性了)
$a’\equiv 1\pmod{3} $
$a’\equiv 0\pmod{5}$
$a’\equiv 0\pmod{7}$
$ =>a’=35p$(可以看到p取2的时候满足$a’\equiv 1\pmod{3}$,即$a’=70$)
接下来要求b’:
$b’\equiv 0\pmod{3}$
$b’\equiv 1\pmod{5}$
$b’\equiv 0\pmod{7}$
$=>b’=21q$(可以看到$q$取1的时候满足$b’\equiv 1\pmod{5}$,即$b’=21$)
现在来看c’
$c’\equiv 0\pmod{3}$
$c’\equiv 0\pmod{5} $
$c’\equiv 1\pmod{7}$
$=>c’=15m$(可以看到m取1的时候满足$c’\equiv 1\pmod{7}$,即$c’=15$)
有了$a’ b’ c’$之后就可以得到 $x = 2a’ + 3b’ + 2*c’ $
代入$a’ b’ c’$之后就可以得到$x$的一个解及其通解
$x = 270 + 321 +2*15 $
$x = 233 + 105t$
在知道同余的加性和乘性之后再看下面这个公式就没有什么问题了
$x \equiv (a_1M_1M_1^{-1} + a_2M_2M_2^{-1} + … + a_kM_kM_k^{-1}) \mod M$
其中,$a_i$就是题目所要求的剩余,$M_1$就是前文提到的标记取法FLAG,而$M_1^{-1}$就是在同余的乘法性中为了满足$a_1’\equiv 1 \pmod{m_i}$
威尔逊定理
当且仅当p为素数时有,
$(p−1) ! \equiv −1\pmod{p}$
证明:
首先:
$p−1 \equiv −1\pmod{p}$
那么我们只需要证明 $(p−2)!\equiv 1\pmod{p} $
也就是说,除去 $1$ 后,如果 $2,3,…,p−2$ 能够两两配对,且每对数乘积模 $p$ 后为 $1$ 的话,威尔逊定理就成立了,然后我们考虑这其实就是对于$ 2,3,…,p−2$去找 模 $p$ 意义下的逆元。
然后考虑一下二次剩余里面的衍生知识,我们可以知道对于 $x^2\equiv 1\pmod{p}$只有两个解$(1,p-1)$,而这两个数已经被我们安排掉了,也就是说 $2,3,…,p−2$中不存在某个数的逆元是自己本身。
然后 集合$ A={1,2,3,…p -1}$; 构成模p乘法的缩系,即任意$i∈A$ ,存在$j∈A$,使得: $( i,j ) \equiv 1\pmod{p}$
也就是说,除去$1$和$p-1$外,其余的两两配对互为逆元
证毕
应用:Rabin算法
在解Rabin算法前,我们需要一些定理、推论
定理1
欧拉判别定理, c是模p的平方剩余的充要条件是 ,$(c^\frac{1}{2})^{φ(n)} \equiv 1\pmod{p}$
证明:
首先,由于$p$是一个奇素数,由费马小定理,$d^{p-1} \equiv 1 \pmod{p}$。但是$P-1$是一个偶数,所以有
$(d^{ \frac{p-1}{2} } -1) \cdot (d^{ \frac{p-1}{2} }+1) \equiv 0 \pmod{p}$
$p$ 是一个素数,所以$d^{ \frac{p-1}{2} } -1$ 和 $d^{ \frac{p-1}{2} }+1$中必有一个是$P$ 的倍数。因此$d^{ \frac{p-1}{2} }$模$P$的余数必然是1或-1。
- 证明若$d$是模$p$二次剩余,则$d^{ \frac{p-1}{2}} \equiv 1 \pmod{p}$
若$d$是模$p$二次剩余,则存在 $x^2 \equiv d \pmod{p}$,$p$跟$d$和$x$ 互质。根据费马小定理得:
$d^{ \frac{p-1}{2}} \equiv x^{p-1} \equiv 1 \pmod{p}$
- 证明若$d^{ \frac{p-1}{2} } \equiv 1 \pmod{p}$,则$d$是模$p$的二次剩余
$p$ 是一个奇素数,所以关于$p$的原根存在。设$a$是$p$的一个原根,则存在$1 \le j \le p-1$使得$d=a^j$。于是
$d^{ \frac{p-1}{2}} \equiv x^{p-1} \equiv 1 \pmod{p}$
$a$是$p$的一个原根,因此$a$模$p$的指数是$p-1$,于是$p-1$整除 $\frac{ j(p-1) }{2}$ 。这说明$j$是一个偶数。令 $i = \frac{j}{2}$ ,就有 $(a^i)^2 =a^{2i} = d$ 。$d$是模$p$ 的二次剩余
定理2
二次同余式$x^2 \equiv c \pmod{p}$的解为:
$ x \equiv ±c^\frac{p+1}{4} \pmod{p} $
证明
由于p是素数,显然a与p互素,再由欧拉判别定理, a是模p的平方剩余的充要条件是 ,
$(c^\frac{1}{2})^{φ(n)} \equiv 1\pmod{p}$
即$(c^\frac{1}{2})^{p-1} \equiv 1\pmod{p}$
带入原式,得$x^2 \equiv c·(c^\frac{1}{2})^{p-1} \equiv c^\frac{p+1}{2} \equiv (c^\frac{p+1}{4})^2$
则
$x \equiv ±c^\frac{p+1}{4} \pmod{p}$
定理3
如果整数$c$满足:
1) $c$为$p$的平方剩余
2) $c$为$q$的平方剩余
则:$ c$为$p*q$的平方剩余,解$x$为:
$x\equiv±(c^\frac{p+1}{4}\pmod{p})\cdot(q^{-1}\pmod{p})\cdot q ± (c^\frac{q+1}{4}\pmod{q})\cdot (p^{-1}\pmod{q})·p\pmod{p\cdot q}$
证明
二次同余式: $x^2 \equiv c\pmod{p*q}$
等价于同余式组 : $x^2 \equiv c \pmod{p}$ ①
$x^2 \equiv c\pmod{q}$ ②
由定理2
①式解为 $x \equiv ±c^\frac{p+1}{4} \pmod{p} $
②式解为 $x \equiv ±c^\frac{q+1}{4} \pmod{q}$
由CRT,解为 $x\equiv±(c^\frac{p+1}{4}\pmod{p})\cdot(q^{-1}\pmod{p})\cdot q ± (c^\frac{q+1}{4}\pmod{q})\cdot (p^{-1}\pmod{q})·p\pmod{p\cdot q}$
Rabin加密
选择两个大素数$p$和$q$做为私钥
计算$n = p * q$做为公钥
若明文为m,则密文为$c \equiv m^2 \pmod{n}$
Rabin解密
我们首先计算出x1和x2,使得
$x_1^2 \equiv c \pmod{p}$,①
$x_2^2 \equiv c \pmod q)$,②
i)p和q都是模4余3的数
由于$p$是素数,显然$c$与$p$互素,再由定理2
得
$x_1 \equiv ±c^\frac{p+1}{4} \pmod{p}$
$x_2 \equiv ±c^\frac{q+1}{4} \pmod{q}$
(一正一负,负的计算可简化为 模-正,如:$-x_1 \equiv p - x_1 \pmod{p}$)
从这里可以看出来如果$p$和$q$不是模$4$余$3$的话,c的指数就不是一个整数,也就不能用这个方法计算了
接着我们求出$p$在模$q$下的逆,设为$a$,即$a*p \equiv 1\pmod{q}$
然后我们求出$q$在模$p$下的逆,设为$b$,即$b*q \equiv 1 \pmod{p}$
求出来a,b用于中国剩余定理
带入 $x\equiv±(c^\frac{p+1}{4}\pmod{p})\cdot(q^{-1}\pmod{p})\cdot q ± (c^\frac{q+1}{4}\pmod{q})\cdot (p^{-1}\pmod{q})·p\pmod{p\cdot q}$
得 $x \equiv±(c^\frac{p+1}{4}\pmod{p})·b\cdot q ±(c^\frac{q+1}{4}\pmod{q})\cdot a·p \pmod{n}$
设$c^\frac{p+1}{4}\pmod{p} $为$cp$,$c^\frac{q+1}{4} \pmod{q}$为$cq$
$x_1 = (b \cdot q \cdot c_p+a \cdot p \cdot c_q ) \mod n$
$-x_1 = n - x_1$
$x_2= (b \cdot q \cdot c_p- a \cdot p \cdot c_q) \mod n$
$-x_2 = n - x_2$
其中有一个为我们想要的明文m。
exp:
1 | import gmpy2 |
ii)p和q不是模4余3的数
这里涉及 Cipolla’s algorithm ,先知已经有一篇讲的不错的文章了
题目实例
UNCTF - 一句话加密
题目是给了一张图,隐写了一个模n
1 | n = 0xc2636ae5c3d8e43ffb97ab09028f1aac6c0bf6cd3d70ebca281bffe97fbe30dd |
可以发现n不大,直接用yafu分解可得
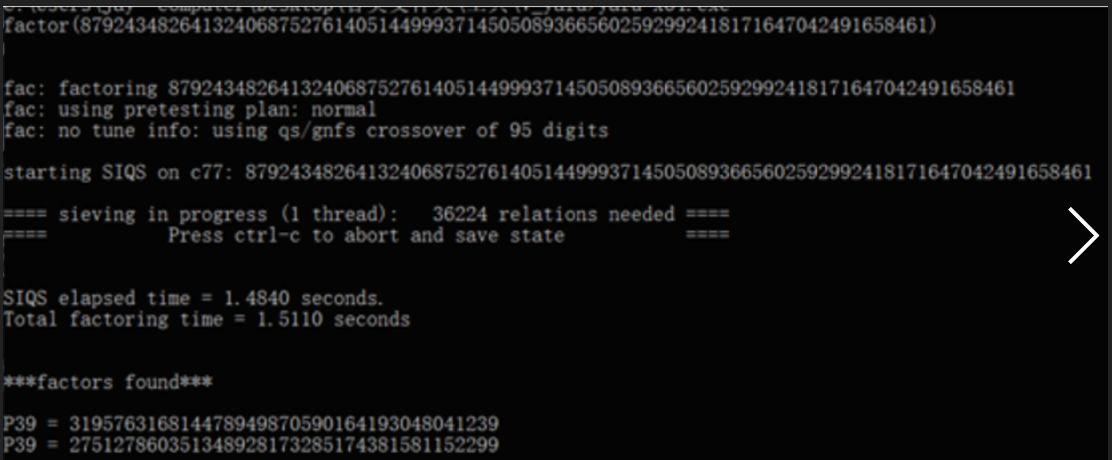
但是找不到e,最后试了试rabin,成功破解
exp用上面的那个就可
roarctf - babyrsa
1 | import sympy |
加密中的(B!)%A的 ! 在这里是阶乘的意思,所以显然这里要用到威尔逊定理,不然这么大的一个数的阶乘,根本吃不消好吧
根据加密逻辑,这里是一个三素数系统,所以$φ(n) = (p-1)(q-1)(r-1)$,然后$r$肯定是要通过先求出$p,q$来得出
然后关于$p$和$q$,题目给的信息都一样,所以求$p$和求q的解法肯定是一样的,
所以题目简化为,根据A1,B1解p
而$p \equiv (B!) \pmod{A}$ (B是一个比A小的数)
虽然A,B均已给出且互素,但显然大数$B$的阶乘是不可能直接求得的,
所以要用威尔逊定理简化计算
简化过程如下:
已知 $B! \equiv P\pmod{A})$
由于A是素数,所以有: $(A-1)! \equiv -1 \pmod{A}$
即$(A-1)(A-2)……(B+1)B! \equiv -1 \pmod{A}$
根据已知$(A-1)(A-2)……(B+1)P \equiv -1 \pmod{A}$
变形为$(A-2)……(B+1)P \equiv 1 \pmod{A}$
所以$p$即为$(A-2)(A-3)……(B+1)$ 在模$A $下的逆
exp
1 | from gmpy2 import * |
HECTF - easy_rsa
1 | from gmpy2 import * |
题目给了,nothing(下面记为r),something(下面记为s),其中$ (p-1)*d= s - r$
目的很明确,就是分解大数n
这一题的思路就是利用$GCD$来约出$n$的因子
所以首先要获得一个$p$的倍数
根据费马小定理
$2^{p-1} \equiv 1 \pmod{p}$显然成立 (主要是为了利用题目中给出的$ (p-1)*d$)
所以设$A = 2^{p-1} - 1 = kp$
然后利用欧拉定理,我们直接利用上文中提到的RSA的解密证明中的结论

$(2^{p-1})^{ed} \equiv (2^{p-1}) \pmod{n}$
由题,$(p-1)d = s - r$
所以$A \equiv 2^{p-1} - 1 \equiv (2^{p-1})^{ed} - 1 \equiv 2^{es-er} - 1 \pmod{n}$
所以 $gcd( 2^{es-er} - 1 , n) $
即 $gcd(kp , pq) $
即可得到 $p$
exp:
1 | import libnum |
构造GCD
可以看出,构造gcd来求大数n的因子以此来分解n是一种很好又很巧妙的方式,来看这一题
1 | from Crypto.Util.number import getPrime, isPrime, getRandomNBitInteger |
这里,我们要通过已给出的a和b,来分解n
通过a,b和p,q的关系,我们要想办法用a,b凑出一个GCD来求出n的一个因子
解题过程如下:
由$ a \equiv (p+q)^{2019} \pmod{n}$
可得 $a \equiv (p+q)^{2019} \equiv p^{2019} \pmod{q}$ 【二项式展开定理】
由$ b \equiv (p+2019)^q \pmod{n}$
可得 $b \equiv (p+2019)^q \equiv p+2019 \pmod{q}$ 【费马小定理:$(p+2019)^q-1 \equiv 1 \pmod{q}$】
所以$ a \equiv (b - 2019)^{2019} \pmod{q}$
即$ a = (b - 2019)^2019 + kq$
这样我们就可以凑出一个$GCD$
$GCD( (b - 2019)^{2019}-a,n)= GCD( Kq,n)= q$
解题完毕
总结
这一次学习了数论四大定理的证明、应用,以及rabin密码的解法。发现其实很多解法、攻击方法都是多种定理的结合运用,有时候还要引出各种推论,很灵活
参考
欧拉定理证明: https://www.cnblogs.com/wangxiaodai/p/9758242.html
中国剩余定理证明: https://blog.csdn.net/Rain722/article/details/53230707
威尔逊定理证明: https://www.cnblogs.com/Judge/p/10755703.html
Rabin算法: https://veritas501.space/2017/03/01/%E5%AF%86%E7%A0%81%E5%AD%A6%E7%AC%94%E8%AE%B0/
https://en.wikipedia.org/wiki/Rabin_cryptosystem
https://blog.csdn.net/qq_24451605/article/details/45093911
最后感谢Lur大佬的一手指点
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081,也可以邮件至 643713081@qq.com
文章标题:密码学学习笔记 之 数论四大定理及应用
文章字数:4.1k
本文作者:Van1sh
发布时间:2019-12-03, 15:30:25
最后更新:2020-06-05, 13:45:42
原始链接:http://jayxv.github.io/2019/12/03/密码学学习笔记之数论四大定理及应用/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

